| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 특성스펙트럼
- 라만 현상
- X선의 발견
- 일상
- 륀트겐
- Raman
- 그루데 이론
- X선
- 라만 분석기
- 빛의 손실
- 재료과학
- 전자의 속도
- 에너지 역학
- 슬립계
- X선 공학
- 분해전단응력
- von laue
- laue
- 화합물 반도체
- 흡광
- 라만 분석
- 결정립
- X선 기초
- 결정구조학
- drude
- 에디슨의 패배
- 전기장이 가해진
- 3 o'clock things
- 연속스펙트럼
- 재료열역학
- Today
- Total
공머생의 공부노트
구면삼각형의 코사인법칙 유도 본문
구면삼각형의 제 1 코사인법칙
구면삼각형 ABC가 있다고 할 때 A점은 좌표계 상에서 z축 위에 존재한다. 이때 AB호가 존재하는 평면과 AC호가 존재하는 평면이 이루는 사이각은 A가 된다.
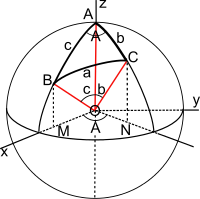

이때 OB와 OC를 크기가 1인 벡터라고 한다면 각 요소는
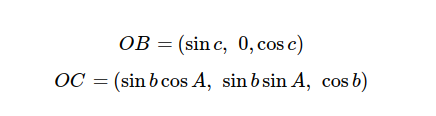
가 되며 OB와 OC사이의 각은 a이므로
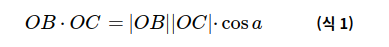
내적에 의해 식 1이 성립하고 식을 정리하면
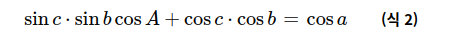
식 2가 유도되며 이를 코사인 1법칙이라고 한다. 이는 cos a 뿐만이 아닌 cos b, cos c 에 대해서도 성립한다.
구면삼각형의 제 2 코사인법칙
제 2 코사인법칙을 유도하기 위해서는 극삼각형의 보각 정의를 사용해야 한다. 극삼각형은 구면삼각형의 각 호를 포함하는 평면의 중점에서 수직한 선을 그려 구와 맏닺는 극(pole)중에서 원래 점에서 가까운 점을 새로운 극점으로 삼아 만들어지는 삼각형이다.

위의 그림에서 BC를 포함하는 평면의 대원의 중심에서 수직하게 그은 선이 구와 만나 만들어지는 점을 극점 A’으로 정의할 때 B’, C’도 같은 방식으로 형성하여 만들어지는 A’B’C’가 ABC에 대한 극삼각형이 된다.
이때 두 구면삼각형 ABC와 A’B’C’사이에는 다음이 성립한다.
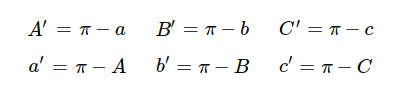
극삼각형 A’B’C’ 또한 코사인 제 1법칙이 성립하므로 식3 또한 성립한다.
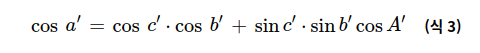
식 3의 값들은 ABC와 A’B’C’사이의 관계식을 이용하여 계산할 수 있으며 식을 전개하면 식4가 성립한다.
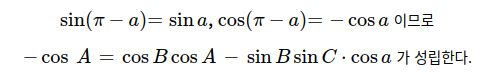

이를 코사인 제2법칙이라고 한다. 이를 통해 a, b, c와 A, B, C사이의 관계식을 유도할 수 있다.
Reference
Spherical Trigonometry: For the Use of Colleges and Schools, Todhunter, I. (Isaac), 1820-1884

