| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- laue
- 에디슨의 패배
- 흡광
- 라만 분석기
- 그루데 이론
- von laue
- 재료열역학
- X선 기초
- 에너지 역학
- 결정립
- 분해전단응력
- X선 공학
- 전자의 속도
- X선
- 화합물 반도체
- 재료과학
- 라만 분석
- 3 o'clock things
- 일상
- 전기장이 가해진
- Raman
- 결정구조학
- 연속스펙트럼
- drude
- 특성스펙트럼
- X선의 발견
- 라만 현상
- 빛의 손실
- 륀트겐
- 슬립계
- Today
- Total
공머생의 공부노트
구면삼각형 본문
구면삼각형이란?
결정학에서 회전대칭에 대해 다룰 때는 3차원 공간상에서 축간의 각을 기하학적으로 고민해야 하는 순간이 많은데 구면삼각형을 활용하면 조금 더 간단하게 생각할 수 있다. 앞으로의 계산을 위해 구면삼각형의 성질에 대한 이해가 필요하기에 짧게 다룬다.
구면삼각형은 말 그대로 구 위에 있는 삼각형을 의미한다. 평면상에 존재하는 삼각형은 3꼭짓점이 평면상에 있기에 세 각의 합이 180도가 되지만 구면삼각형에서는 기울어진 구면 위에 있기에 그 합이 180도가 아니게 된다. 이러한 평면상에 존재하지 않는 기하를 비유클리드 기하라고 하며 우리가 일반적으로 사용하는 방식과 다른 방식을 사용해서 접근해야 한다.

구면삼각형을 다룰때는 항상 내가 얻고자 하는 점에 대한 정보가 원 표면에 있다는 것을 생각하며 표면을 지나는 원주를 그려 해결하는 것이 효율적이다.
구면삼각형의 성질
1) 구면삼각형의 변들은 대원에 속해있다.
3차원 구의 표면에 원이 있다고 가정할 때 원의 반지름이 구의 반지름과 같다면 대원(great circle) 그렇지 않다면 소원(small circle) 이라고 한다. 대원은 어떤 각도로도 존재할 수 있다.


이때 구면삼각형의 변들은 항상 대원의 일부가 된다. 구면삼각형을 만들기 위해 A, B, C 세 점을 찍고 삼각형을 만들기 위해 구를 따라 선을 그리면 그 선은 항상 호가 되며 호는 항상 구의 중심점을 지나는 원의 일부가 된다. 이는 대원을 의미하고 결국 어떤 식으로 삼각형을 만들어도 구면삼각형의 변들은 대원에 속한다.
2) 구면삼각형에서 축간 결합각도는 호의 길이와 같다.
구면삼각형에서 구의 반지름 길이는 1이다. 그러므로 호도법에 따라 호의 길이는 라디안으로 표시된 각의 크기와 같다.(아래 그림과 같다) 그러므로 OA, OB사이 각은 c가 되며 OB, OC사이 각은 a OC, OA사이 각은 b가 된다.

3) 구면삼각형의 세 각의 합은 180˚보다 크고 540˚보다 작다.
비유클리드 기하에서 삼각형의 세 각의 합은 항상 180˚이지만 곡면 위에 있는 구면삼각형은 자체가 기울어져 있다. 그러므로 세각의 합은 180˚가 아니게 되는데 세 각의 합을 알아내는 것은 이해가 쉽지 않다.
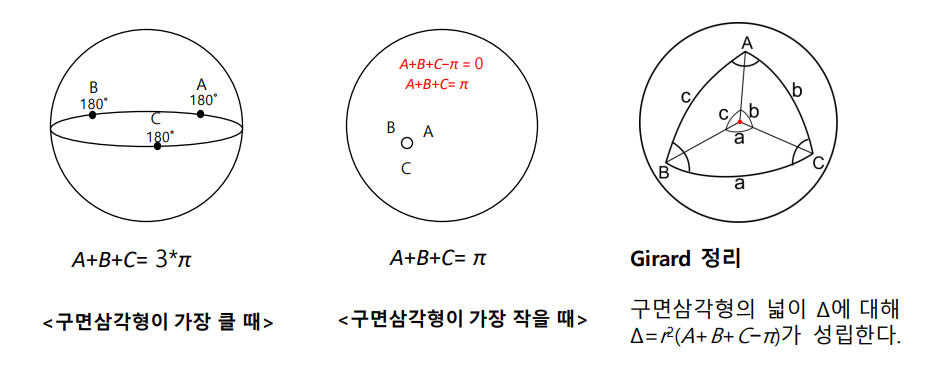
구면삼각형에서 세각의 합이 가장 클 때는 구면삼각형이 가장 크게 펼쳐질 때, 즉 구면삼각형 자체가 대원이 되었을 때가 된다. 이때 각은 직선이 되므로 한 각당 180˚가 되고 각이 3개이므로 540˚가 된다.
세각의 합이 가장 작을 때는 구면삼각형이 가장 작게 펼쳐질 때 인데 이는 구면삼각형의 넓이를 통해서 이해할 수 있다. 구면삼각형이 가장 작아진다면 구 위에서 점이 되고 이때 넓이는 0이 된다. 이때 구면삼각형의 넓이는 girard 정리에 따라(r=1) A+B+C-PI=0이 되고 이에 따라 세 각의 합은 180˚이 된다.
Reference
https://jjycjnmath.tistory.com/312
'물리학 > 구면기하' 카테고리의 다른 글
| 구면삼각형의 코사인법칙 유도 (0) | 2023.04.01 |
|---|

