| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 전기장이 가해진
- 분해전단응력
- 라만 분석기
- 전자의 속도
- 라만 현상
- 라만 분석
- 슬립계
- 일상
- X선 기초
- 흡광
- 륀트겐
- 재료과학
- 결정립
- 3 o'clock things
- Raman
- von laue
- 특성스펙트럼
- 빛의 손실
- 연속스펙트럼
- drude
- 에디슨의 패배
- 화합물 반도체
- laue
- 재료열역학
- 결정구조학
- X선
- X선 공학
- 그루데 이론
- X선의 발견
- 에너지 역학
- Today
- Total
공머생의 공부노트
교류회로-L만의 회로 본문
2. 인덕턴스만의 회로
인덕턴스는 코일로 이루어진 회로요소로서 전압이 증가하면 그 전압에 대항하여 역 기전력(L-emf)를 형성하는 특징이 있다. 인덕턴스에 전압이 가해지면 렌츠의 법칙에 의해 그 전압을 상쇄하는 방향으로 역전압이 형성되고 이때 그 전압의 크기는 코일의 자속의 변화율과 감긴 수에 비례한다.
$$V_{L} = -N\frac{d\phi}{dt}$$
이때 자기유도의 원리에 따라 자체 인덕턴스 비례상수인 L은 코일의 감긴수와 자속에 비례하고 전류에 반비례 하므로
$$L = \frac{N\phi}{I}$$
결국 인덕턴스의 전압은 비례상수인 L과 전류의 변화율에 비례한다.
$$V_{L} = -N\frac{d\phi}{dt}=-L\frac{dI}{dt}$$
인덕턴스 1개만이 존재하는 회로에서 전압이 증가함에 따라 인덕턴스에 걸리는 전압도 V = Vmsin(wt) 로 증가하는데 그렇다면 아래 식이 성립하고
$$V_{m}sin(wt)=L\frac{dI}{dt}$$
$$\frac{dI}{dt} = V_{m}sin(wt)$$
$$I = -\frac{V_{m}}{Lw}cos(wt)$$
이때 -cos(wt)는 sin(wt-1/2)와 같으므로
$$I = \frac{V_{m}}{Lw}sin(wt-\frac{1}{2}\pi)$$
인덕턴스에 걸리는 전압은 V = Vmsin(wt)이며 전류의 값은 I = V/Lw sin(wt-1/2)가 된다. 즉 전류의 위상은 전압보다 1/2PI 빠르다.
2-1. 인덕턴스만의 회로 시뮬레이션
교류전원(V=Vmsin(wt))이 인덕턴스에 그대로 연결되어 있고 교류전원의 주파수는 60HZ, 최대 전압은 1V이다. 1/60초(0.016s)에 1주기가 지나가므로 0초부터 0.03초 사이를 확인한다.

실제 코일로만 구성된 회로에서 인덕턴스의 전압이 전압기의 전압이 같다는 것과 전류의 위상이 전압보다 90도 느리다는 것을 알 수 있다.

전류 공식에 따라 전류의 크기는 전압에 비례하고 L과 w(주파수 2πf=w)에 반비례 한다.
$$I = \frac{V_{m}}{Lw}sin(wt-\frac{1}{2}\pi)$$
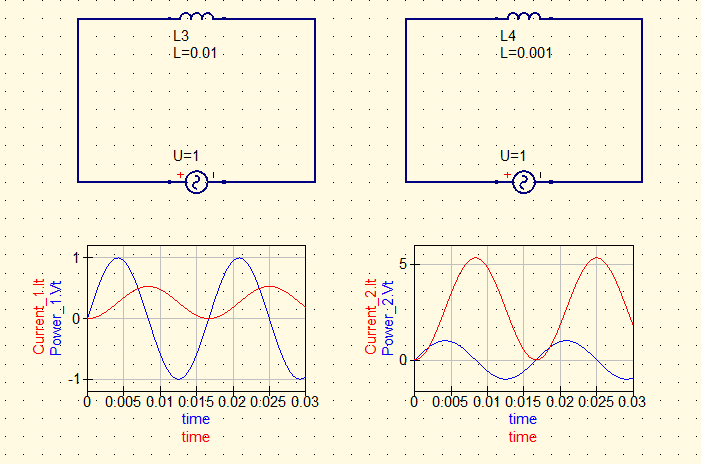
인덕턴스가 10mH인 회로와 1mH인 회로를 비교해보면 실제로 전류 값이 10배 차이 나는 것을 확인 할 수 있다. 또한 인덕턴스는 저항이 없는 회로이므로 이상적으로 에너지 손실이 존재하지 않는다.
'전자공학, 프로그래밍 > 전자공학 이론' 카테고리의 다른 글
| 교류회로-C만의 회로 (0) | 2023.07.15 |
|---|---|
| 교류회로-R만의 회로 (0) | 2023.07.15 |
| Voltage Divider (전압 분배기) (0) | 2022.05.08 |
| Voltage Drop (전압 강하 효과) (2) | 2022.05.08 |
| 축전기 (0) | 2022.03.30 |




