| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 화합물 반도체
- 라만 분석기
- 결정립
- 에디슨의 패배
- 슬립계
- 라만 현상
- 일상
- 전자의 속도
- 특성스펙트럼
- 흡광
- 재료과학
- 에너지 역학
- von laue
- 라만 분석
- 분해전단응력
- X선
- X선 공학
- X선 기초
- drude
- 재료열역학
- 전기장이 가해진
- 연속스펙트럼
- 결정구조학
- Raman
- 그루데 이론
- 륀트겐
- X선의 발견
- laue
- 빛의 손실
- 3 o'clock things
- Today
- Total
공머생의 공부노트
시간에 무관한 슈레딩거 방정식 본문
일반적으로 제시되는 schrodinger방정식은 특정한 퍼텐셜 V(x,t)에 대하여 아래의 방정식을 성립한다. 결국 슈레딩거 방정식은 2차 편미분 방정식을 해석해야 하므로 ψ(x,t) = ?? 인가에 대한 고민에 중점이 맞춰져 있다. 이때 ψ는 x와 t에 대한 식으로서 공간과 시간에 대한 고려를 동시에 포함해야 한다.
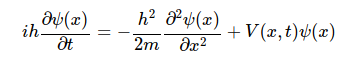
다만 우리가 관심있는 일반적인 상태에서는 t 가 식에 영향을 끼치지 못하는 즉, 정상상태(steady state)에서의 ψ에 대해 고민할 필요가 있다.
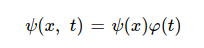
Ψ를 변수분리 하여 전개하게 되면 ψ는 x만의 함수로 정의하고 φ는 t만의 함수로 정의 가능하다. 이때 식에 이를 적용하여 바로 풀이하면
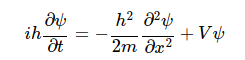
위에 식에 ψ = ψ* φ를 적용하면

또한 전체 식에 ψ*φ를 나누면
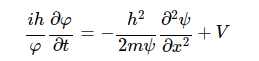
위 식으로 전개되는데 식의 좌변은 t에 대한 식이며 우변은 x에 대한 식이다. 그렇다면 t 혹은 x의 한쪽에 변화에 따라 한쪽 항은 틀린 값이 되므로 위 식이 성립되는 것은 그 두 항이 모두 상수일 때
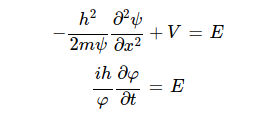
위와 같은 식일때만 성립된다. E 는 임의로 정한 상수이다. 이때의 E 는 아무 의미 없이 정한 상수이지만 실제 위의 상수항은 에너지를 나타내므로 E라고 표현하는 건 우연이 아니다.
(1) 시간에 대한 함수
슈레딩거 방정식은 x와 t에 대한 방정식인데 위의 2개의 방정식중 아래의 방정식이 시간에 대한 함수가 된다. 1계도 미분방정식이므로 φ(t)=e^at 꼴의 함수가 그 해가 될 것이다.
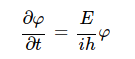
이를 대입하여 a를 구하면
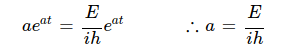
그러므로 슈레딩거 방정식에서 시간에 대한 함수는 아래와 같이 구해진다.
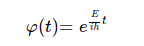
이때 위의 시간에 대한 함수는 확률밀도를 구할 때 ψ(x)값에 무관하게 스스로 사라지게 된다. 이것 때문에 변수분리가 가능한 모든 슈레딩거 방정식은 정상상태, 즉 시간에 무관한 특징을 가지게 된다.
(2) 위치에 대한 함수
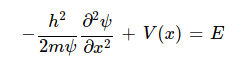
포텐셜의 함수 개형이 달라짐에 따라 식의 해석이 완전히 달라지므로 시간에 대한 함수처럼 정해진 함수가 구해지지 않는다. 또한 2계도 미분 방정식이므로 V(x)에 따른 해석이 개별적으로 진행되야 한다.
이때 변수분리가 가능한 함수에는 물리적으로 3가지 특징이 있는데 1. 정상상태이며 2. 파동함수당 1개의 명확한 에너지를 가지며 3. 그 일반해는 변수분리한 해의 선형결합으로 이루어 진다.
'물리학 > 양자역학' 카테고리의 다른 글
| 흑체 복사와 레일리 진스 법칙 유도 (0) | 2025.02.15 |
|---|---|
| 무한한 사각형 우물 해석하기 (0) | 2023.01.24 |


