| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 |
- 슬립계
- X선
- 화합물 반도체
- Raman
- 에너지 역학
- 특성스펙트럼
- 재료과학
- 연속스펙트럼
- 일상
- von laue
- 재료열역학
- 에디슨의 패배
- 그루데 이론
- X선 공학
- 륀트겐
- 흡광
- 전기장이 가해진
- 분해전단응력
- 빛의 손실
- 결정립
- 라만 분석기
- 라만 분석
- X선 기초
- laue
- 전자의 속도
- drude
- 라만 현상
- X선의 발견
- 3 o'clock things
- 결정구조학
- Today
- Total
공머생의 공부노트
아두이노를 활용한 UV-VIS분석기 만들기 (PART 1. 분석법의 기본 원리) 본문
분광분석법이란?
일반적으로 빛과 물질의 상호작용을 통한 분석을 하는 분석법중 하나로, 이전에는 가시광선(VIS), 자외선(UV)영역에서의 연구가 이루어졌지만 최근에는 빛의 범위를 늘려 방사선이나 X-ray등의 파장을 활용하는 분광법도 나오고 있다.
분광분석을 통한 시료의 분석은 가장 강력한 Tool중 하나로 시료의 손상 없이 타겟 물질의 정령, 정성적인 분석을 가능하게 한다는 장점이 있다. 이번 실험 설계에서는 UV-VIS Spectrophotometry를 중점으로 전개해 나가고자 한다.

분광분석법의 기본 원리
분광분석은 크게 정량분석과 정성분석으로 나뉘는데, 정량분석은 시료의 양을 파악하고 정성분석은 시료의 종류를 파악하게 된다. 특정 파장의 빛이 시료를 통과하게 된다면 시료는 그 빛을 흡수하게 된다. 시료에 입사된 빛은 흡수(Absorbed), 반사(Reflected), 투과(Absorbed), 산란(Absorbed) 등의 4가지 상호작용을 하게 된다. 결과적으로 (입사된 빛의 세기 = 흡수+반사+투과+산란의 세기) 가 성립하게 된다.

여기서 투과와 흡수를 중점적 해석을 하게되면 다음과 같이 상황을 단순화 할수 있다. 이때 산란과 반사는 무시된다.

투과도와 흡광도의 정의
입사된 빛이 시료를 지나게되면 시료는 그 빛을 흡수하게 되는데 I0>I가 항상 성립하게 된다. 이때 투과된 빛의 세기를 입사된 빛으로 나눈 것을 투과도(Transmittance)라고 정의한다.
T는 0~1의 범위를 지니며 실제로는 100T인 퍼센트 투과도(Percent Transmittance)로 변환하여 0~100%로 사용한다.
이때 물질이 빛을 흡수하는 정도인 흡광도에 대한 정보도 필요한데 이 흡광도는 투과도를 상용로그화 한 값이다.
이때 투과도와 흡광도과의 관계는 다음과 같다.

흡광도의 수학적 정의
흡광도와 투과도는 로그관계를 취하고 있는데, 이는 흡광도의 정의에서 기인한다. 얼핏 생각하면 왜 로그의 관계로 설명이 되야하는지 의야할 수 있지만 그 정의를 살펴보면 쉽게 이해할 수 있다.
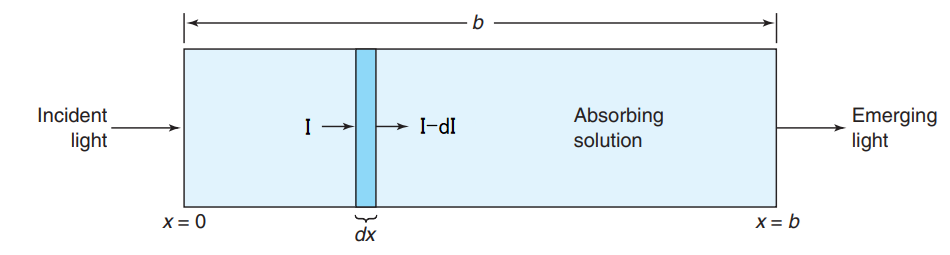
흡광도는 빛의 감소에 따른 물리적 모델을 수학적으로 해석함으로서 얻어진다. 국소구간에 빛이 입사하여 길이가 b인 시료를 빛이 지나친다고 가정하자.
시료의 어느 지점에 국소구간 dx를 지나며 감소한 빛의 양을 dI라고 한다면, dI는 처음 입사한 빛의 세기(I0)와 빛이 통과한 거리(dx), 단위 부피당 물질의 양에 비례하게 된다. 즉 빛이 감소하는 양은 처음 빛이 강할때, 빛이 통과한 거리가 길때, 지나치며 부딛치는 물질이 많을때 더 많이 감소한다는 가정을 세운 것이다. (β는 비례관계에 대한 상수이다)
이때 적분을 통해
결과적으로 시료내의 x위치에서의 빛의 세기는 다음 식으로 전개된다. 이는 이전 포스팅의 x선 흡광과 비슷한 결의 증명 결과임을 확인할 수 있다.
X선의 흡광 (Absorbption)
물질 내를 진행한 X선의 강도는 내부에 있는 물질의 충돌에 의해 점점 감소하는데, 일반적으로 X선의 형광 혹은 산란에 의해 이루어진다. 이를 종합하여 X선의 흡광 이라고 표현한다. X선이 타겟
yumy.tistory.com
위에서 전개한 식을 빛이 입사해서 x=b 지점을 지날 때를 적분하여 입사광과 투과광의 관계로 풀게 되면 다음과 같이 증명할 수 있다.
이때 로그가 취해진 왼쪽 수식을 흡광도로 정의하고 /beta를 흡광계수로 두게 되면 우리에게 익숙한 Lambert-Beer's Law가 구해진다.
다음과 같은 정의로 인해 흡광도는 시료의 길이(b)와 시료의 농도(c)에 비례한다는 것을 수학적으로 정의할 수 있으며 투과도와 흡광도가 왜 로그관계를 가지는지 이해할 수 있다.
[출처]
1. QUANTITATIVE CHEMICAL ANALYSIS Eighth Edition, Daniel C. Harris Michelson Laboratory China Lake, California
'전자공학, 프로그래밍 > 전자공학 실험' 카테고리의 다른 글
| 나의 군대 전자기기기능사 후기 (필기편) (2) | 2023.11.12 |
|---|---|
| PROJECT 3. OP AMP 소자 활용하기 (0) | 2022.02.09 |
| PROJECT 2. 아두이노로 간단한 디지털 멀티미터 만들기 (4) | 2022.02.02 |
| PROJECT 1. Pull up과 Pull down (0) | 2022.02.02 |
| 아두이노를 활용한 UV-VIS분석기 만들기 (PART 2. 분석기의 설계) (20) | 2021.11.13 |





