| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- X선의 발견
- 륀트겐
- 슬립계
- 재료열역학
- 결정구조학
- 일상
- 전기장이 가해진
- 라만 분석
- 에너지 역학
- 빛의 손실
- 에디슨의 패배
- 3 o'clock things
- 전자의 속도
- 라만 분석기
- X선
- 특성스펙트럼
- 흡광
- 분해전단응력
- laue
- 연속스펙트럼
- Raman
- drude
- von laue
- 그루데 이론
- 화합물 반도체
- X선 공학
- 재료과학
- 라만 현상
- 결정립
- X선 기초
- Today
- Total
공머생의 공부노트
결정배위 (coordination) 본문
배위 (coordination)는 "양이온을 음이온이 둘러싸는 것"으로 결정에서 한 원자가 위치한 곳을 설명하기에 편리한 개념이다.
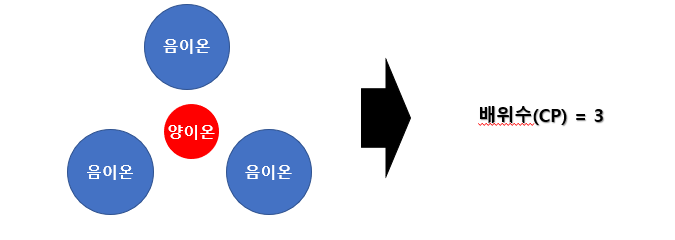
배위수는 CP = n 이라는 표현을 사용하는데, 이는 한 양이온 원자에 공간적으로 음이온이 n개가 가장 안정되게 둘러싼 형태를 의미한다.
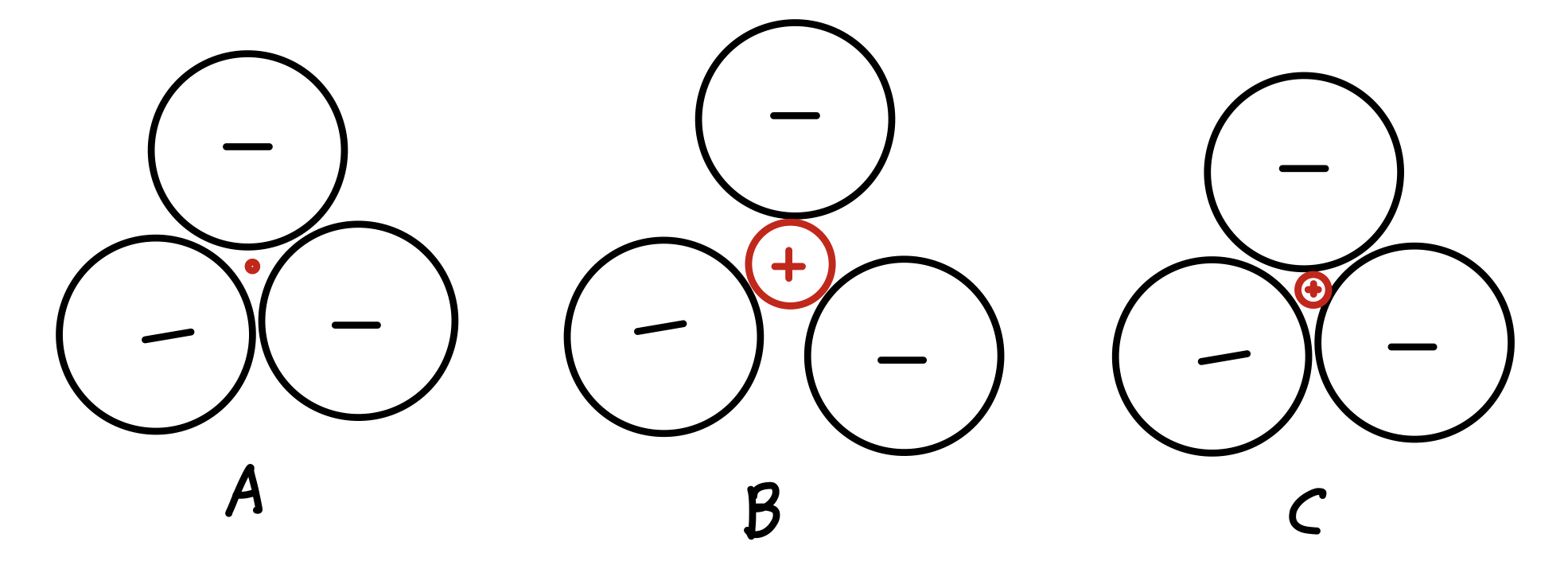
그렇다면 다음 CN = 3 그림에서 가장 안정적인 배위 형태는 무엇일까? A는 양이온의 크기가 작아 음이온들이 서로 접촉하고 있고 B는 양이온의 크기가 커서 음이온과 양이온의 접촉 외에는 다른 접촉이 없다. C는 앙이온 - 음이온, 음이온 - 음이온 모두 접촉한다.
구들이 전하를 가지지 않는 입자라면 C가 거시적인 구조에서는 안정적이지만 위의 그림은 미시세계의 서로 다른 전하를 가진 구들이다. 그러므로 서로 다른 전하가 접촉하고 같은 전하들은 거리를 두는 B의 배위 형태가 가장 안정적이다.
또한 배위수들은 3뿐만이 아니라 n=2 이상의 값을 가질 수 있는데, 각 CN마다 R(양이온)과 R(음이온)의 비를 구해낼 수 있다. (계산을 위해 배위 형태가 C라고 가정한다.)
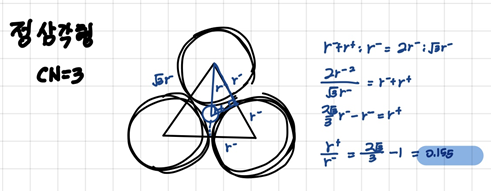
CN = 3 (triangle site)
CN = 4 (tetrahedron site)

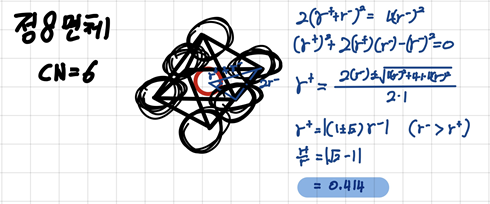
CN = 6 (octahedron site)
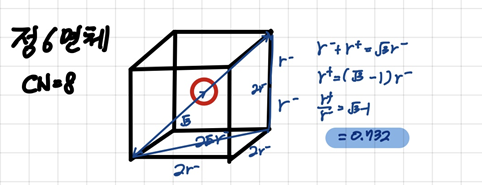
CN = 8 (hexahedron site)
CN = 12 (anti cubo octahedron site)
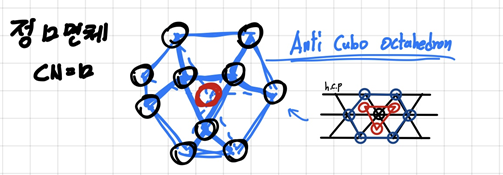
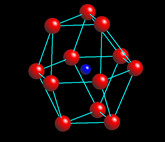
이에 따라 각 CP마다 안정되기 시작하는 양이온/음이온 반지름 비를 추정해낼 수 있다. 위에 예시에서와 같이 C->B로 양이온의 반지름이 커지면 안정되는 것을 꼭 염두에 두자
r+/r- < 0.155 -> CN=2 가 안정적
0.155 < r+/r- < 0.225 -> CN=3 가 안정적
0.225 < r+/r- < 0.414 -> CN=4 가 안정적
0.414 < r+/r- < 0.732 -> CN=6 가 안정적
0.732 < r+/r- < ??? -> CN=8 가 안정적
'재료공학 > 결정구조학' 카테고리의 다른 글
| AmXz의 결정구조 (0) | 2021.06.11 |
|---|---|
| AX2 화합물의 결정구조 (0) | 2021.06.11 |
| AX 화합물의 결정구조 (0) | 2021.06.09 |
| 단원소의 결정구조 (0) | 2021.06.08 |
| 결정화학 (화학결합) (0) | 2021.06.08 |



