| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 결정구조학
- von laue
- 연속스펙트럼
- 재료과학
- 분해전단응력
- 흡광
- 전기장이 가해진
- X선
- 라만 현상
- 슬립계
- 륀트겐
- 화합물 반도체
- 라만 분석기
- 전자의 속도
- X선 기초
- 에너지 역학
- X선의 발견
- 라만 분석
- 재료열역학
- 그루데 이론
- drude
- laue
- 에디슨의 패배
- 특성스펙트럼
- 3 o'clock things
- 일상
- 결정립
- 빛의 손실
- X선 공학
- Raman
- Today
- Total
공머생의 공부노트
1. 격자와 단위포 본문
단원소의 결정구조
단원소 결정에서는 금속결합, 공유결합, van der waals 결합 만 적용되고 이온결합은 적용되지 않는다. 보통 단원소 물질(금속, 과냉각 기체)들은 구밀집 구조를 가진다. 1. hexagonal closed packing (h.c.p.)
yumy.tistory.com
AX 화합물의 결정구조
1. 징크블렌드 (zincblende) - ZnS , GaAs, InP space group : (No. 216) 징크블렌드 구조는 ZnS 화합물의 구조로서 다이아몬드에서 치환된 구조이다. 다이아몬드와 마찬가지로 입방구조의 Zn과 S가 이탈벡터 (1/4,
yumy.tistory.com
이전 블로그에서는 물질의 종류에 따라 어떤 구조를 가지고 있는지에 대해 중점적으로 다루었다. 하지만 정작 왜 이것을 결정으로 표기해야 하는지에 대해서는 자세히 설명하지 않고 기술적인 부분을 중점으로 나타냈다. (특별한 이유가 있는건 아니구.....그냥 그때 마침 이거 하고 있었어서) 하지만 결정구조를 제대로 활용할려면 왜 저 작은 단위포의 원자 배열 만으로 그 물질 전체를 이해할 수 있는지 공부가 필요하다.
1. 격자와 단위포
결정학에서는 격자(lattice)와 단위포(unit)이라는 개념이 가장 핵심적이며 기본이 되는 개념이다.격자와 단위포는 가장 핵심이 되는 개념인 만큼 직관적인 이해가 중요하다. 우선 2차원 평면에서 배열되어 있는 원자를 생각해보자.
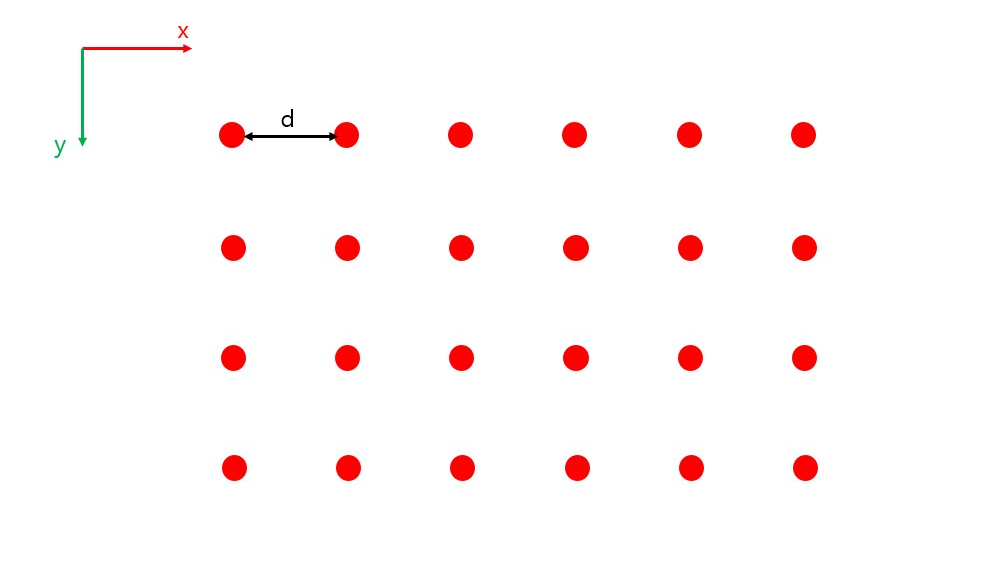
모든 빨간색 원자들은 동일하며 어느 기준으로 봐도 배위수는 4로 같다. 빨간색 원자중 하나가 되어 생각해 본다면 어느 곳에 있든 주변에 보이는 원자가 같다는 소리다.
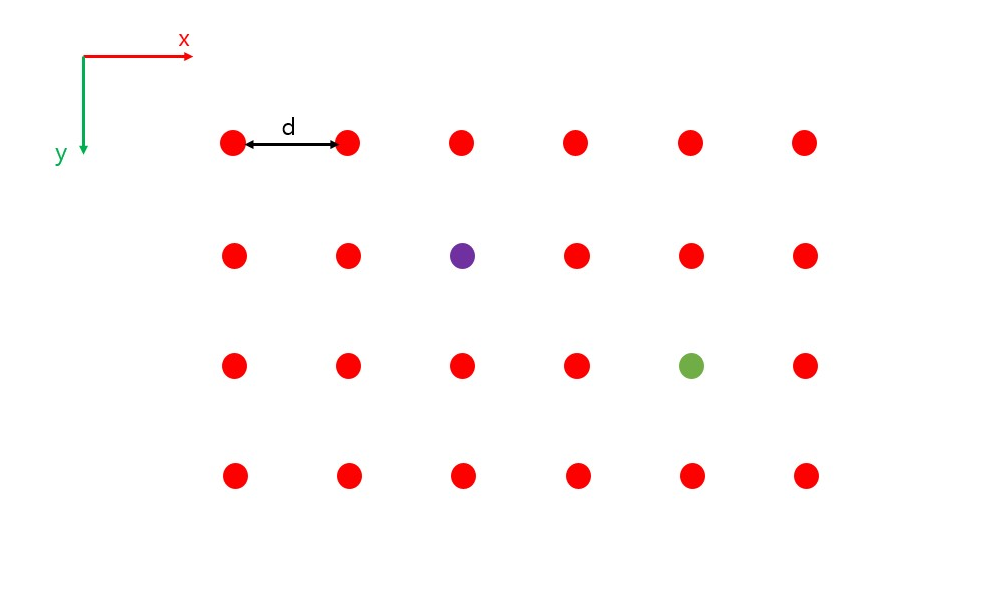
보라색 원자에서 주변을 보든 초록색 원자에서 주변을 보든 주변은 모두 똑같아 보인다.즉 위의 두 원자는 동일한 주위 환경(surrounding)을 가지고 있다. 이는 위의 원자 배열이 규칙성이 있다는 것을 의미하고 자세히 보면 매우 작은 요소가 일정한 규칙으로 반복되는 것을 알 수 있다.
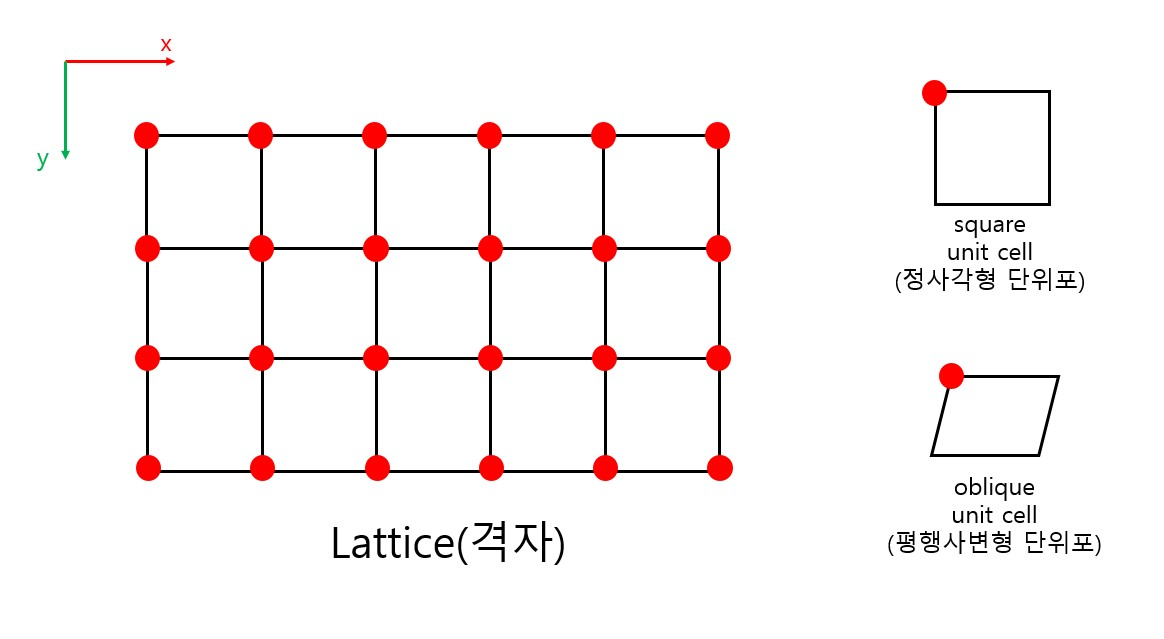
그래서 우리는 원자들의 배열에서 가장 작은 단위를 설정해서 이를 규칙에 따라 대칭이동 시키는 방식으로 결정 전체를 설명한다. 이때 원자의 배열에서 가장 작은 반복단위를 단위포(unit cell)이라 부르고 수많은 단위포의 규칙있는 배열을 격자(lattice)라고 한다.
어떤 한 점의 환경과 동일한 환경을 갖는 점들의 배열을 2차원에서는 망목(mesh or net)이라 하고 3차원에서는 격자(lattice)라고 하며 각각의 점들을 격자점이라 부른다.
또한 단위포란 격자점을 연결하여 만든 2차원에서는 평행사변형, 3차원에서는 평형육면체를 말한다.
이때 반대로 생각해서 격자점으로 부터 단위포를 설정해야 할 때도 있는데 이때 반드시 단위포는 기저 방향(u)에 대한 병진 및 회전 대칭을 생각해서 설정해야 한다. 단위포를 설정했는데 평형이동하여 격자를 형성하지 못한다면 이는 잘못된 단위포 설정이다.
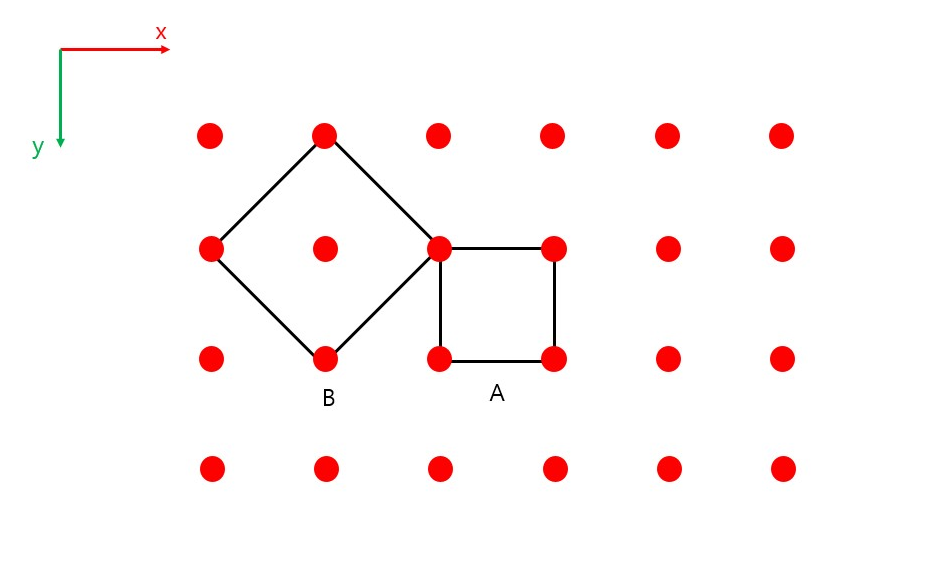
이뿐 만이 아니라 단위포는 위의 그림에서 처럼 A같은 형태로 지정할 수 있지만 더 큰 형태인 B형태로 지정할 수도 있다. 즉 가장 작은 단위라고 해서 반드시 크기가 가장 작은 것에 집착할 필요는 없다는 것이다. A같이 단위셀 내에 격자점이 1개인 것을 단격자 단위포 (Primitive, P-cubic) 이라 하고 B같이 격자점이 2개 이상인 것은 다격자 단위포 ( Nonprimitive, I-cubic)이라고 한다.
2. 단위포와 기저
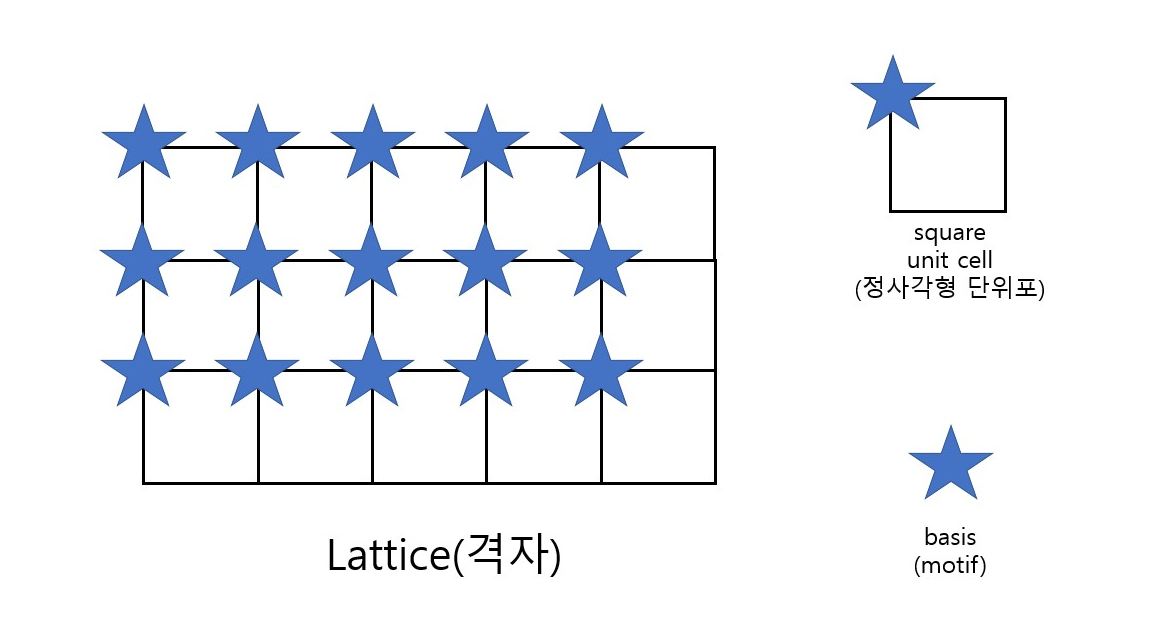
격자는 점들의 집합이므로 결정을 구성하기 위해서는 각 격자점에 어떤 요소를 주어야 한다. 앞선 설명에서는 원자를 격자점으로 대신해서 보여주었지만 격자점은 원자를 의미하는 것이 아닌 대칭의 기준이 되는 요소를 말하는 것이다. 격자를 이루기 위해서는 위의 그림처럼 단위포에 쒸워지는 기저(basis)가 필요하다. 대칭적으로는 단위포가 결정되면 basis가 어떤 모양이라도 격자는 대칭을 이룬다. 그림처럼 별모양의 모양이 있더라도 그것이 단위포의 어떤 위치에 있더라도 상관없다.
기저는 모든 격자점에 동일하게 들어가서 전체 결정을 이루는 원자 집단을 말한다
결정은 격자점의 배열인 격자와 각 격자점에 놓이는 기저로 나타낼 수 있다.
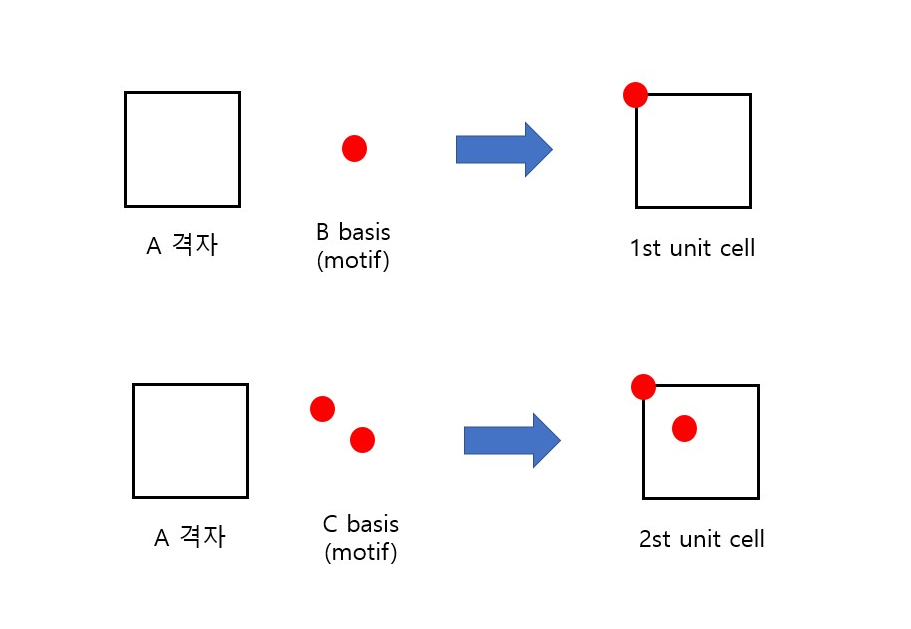
아래와 같이 A격자에 B,C 기저를 결합시키는 경우를 생각해보자. B기저와 A격자의 결합은 단격자 단위포 (Primitive, P-cubic) B기저와 A격자의 결합은 다격자 단위포 ( Nonprimitive, I-cubic)가 될 것이다. 별 모양의 기저가 격자를 이루는 것과 완전히 똑같은 개념이다. 즉 대칭성을 거스르지 않는다면 기저에 해당하는 원자가 어디에 어떻게 존재하든 결정을 이룰 수 있는 것이다.
다만 주의해야 할 점이 있다. 기저의 모양이 어떤 모습이든 상관 없다고 해서 겹치는 원자가 존재해서는 안된다. 대칭성을 거스르지 않는다는 것이 이런 것을 의미하게 된다. 아래의 2번째 그림처럼 결정 전체에서 봤을때 단위포 네 변에 모두 원자가 들어간다고 기저 까지 4개의 원자를 포함하는 것은 아니다. 정사각형 단위포에서는 1개의 원자만이 기저로 존재할 수 있다. 이 1개의 원자가 평행이동을 통해 전체 결정을 형성하는 것으로 받아들여야 한다 (물론 일반적으로 단위포 4개에 원자를 다 집어넣긴 하지만 이건 이해를 쉽게 하기 위함이다)
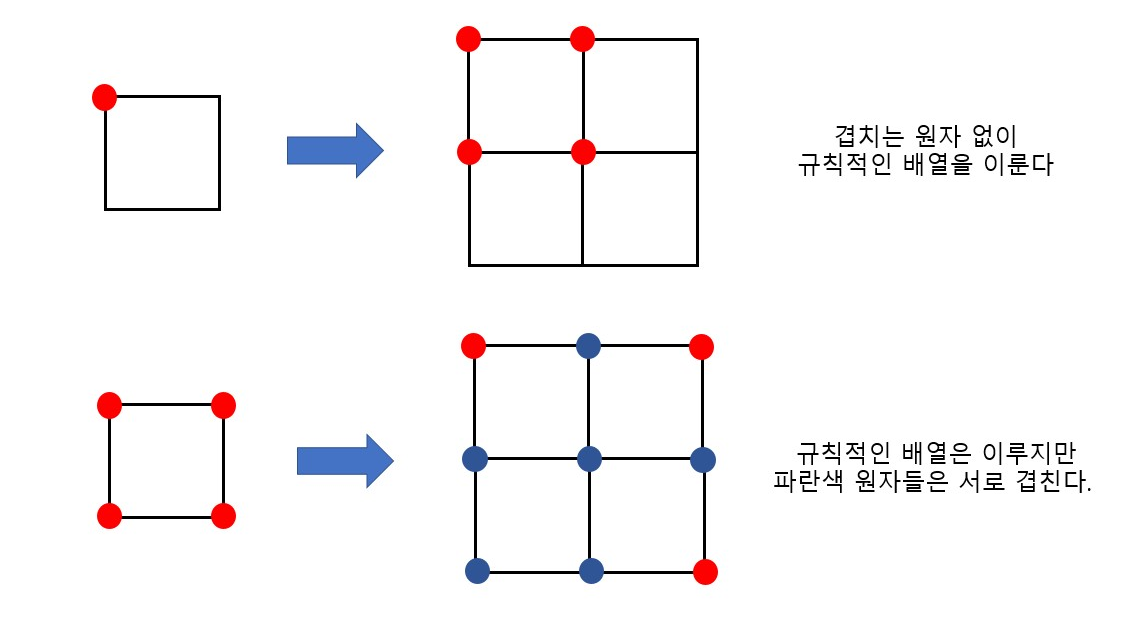
만일 기저에 4개의 원자가 존재한다고 이해해 버리면 회전이동이나 평행이동(병진이동)시 겹치는 원자가 발생한다. 항상 단위포를 기준으로 대칭이동이 성립하는지 확인해야 한다.
'재료공학 > 결정구조학' 카테고리의 다른 글
| 3. 공간상의 대칭 (5가지 회전 대칭) (0) | 2023.03.26 |
|---|---|
| 2. 대칭요소 (0) | 2023.03.26 |
| 규산염의 결정구조 (0) | 2021.06.12 |
| AmBnXz의 결정구조 (0) | 2021.06.11 |
| AmXz의 결정구조 (0) | 2021.06.11 |




