| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 재료열역학
- 분해전단응력
- 라만 현상
- 흡광
- laue
- 라만 분석
- 연속스펙트럼
- X선의 발견
- 륀트겐
- 에디슨의 패배
- Raman
- 슬립계
- drude
- X선
- 에너지 역학
- 재료과학
- 빛의 손실
- 일상
- 라만 분석기
- 특성스펙트럼
- X선 공학
- X선 기초
- 전자의 속도
- 전기장이 가해진
- 화합물 반도체
- von laue
- 결정구조학
- 3 o'clock things
- 결정립
- 그루데 이론
- Today
- Total
공머생의 공부노트
2. 대칭요소 본문
결정에서 원자의 대칭적인 배열은 대칭요소로 표시된다. 사실상 결정구조에 대한 공부는 대칭에 대한 공부와 같다. 실제 원자의 배열에 대해 고민하기 때문에 상당히 직관적이지만 대칭 여러개가 겹치기 시작하면 상당히 머리가 아파진다. 우선 대칭에 대해 정의할 필요가 있다. 존경하는 교수님의 표현을 빌리자면
"대칭이란 변환에 대해 불변이다 !"
조금 더 자세한 정의로는 "어떤 작동(operation)을 하였을때 작동을 한 후의 주위 환경이 작동전의 그것과 일치(coincidence) 되는것을 말한다" 처음 나도 이 정의를 들었을때 이해하는데 시간이 오래걸렸다. 하지만 대칭을 이런 말로 설명하는데는 그럴만한 이유가 있다.
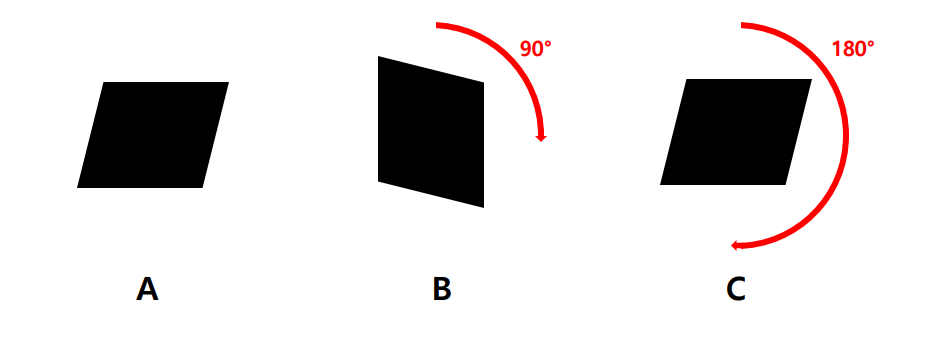
위의 그림처럼 평행사변형 A가 있다고 하자, 만약 우리가 A를 블럭처럼 가지고 놀다가 돌린다고 생각해보자. A를 90도 돌리면 B와 같이 되고 180도 돌리면 C와 같이 된다. 하지만 우리가 A를 180도 돌렸음에도 불구하고 C는 A와 완전히 똑같이 생겼다. 다른 사람이 지나가다 A와 C를 보면 어떤 것이 돌린것인지 구별이 불가능하다. 이것이 대칭의 정의인 변환에 대한 불변이다.

위의 개념을 실제 물질에 대입해서 생각해보면 위의 그림과 같다. 그래핀을 위에서 본 그림을 A라고 하고 30도, 60도로 회전 이동시킨 것을 B, C라고 하자. A와 C는 원자가 끝없이 많이 늘어져 있다면 완전히 같은 그림이 된다. 결국 고개를 얼마나 돌리냐에 따라 보이는것은 똑같다고 할 수 있는 것이다. 이때 여기서 사용한 어떤 작동(operation)은 임의로 설정한 축에 대한 회전이지만 작동은 회전뿐만이 아닌 다른 어느 것도 될 수 있다.
1. 대칭 요소의 종류
1) 병진대칭(translate symmetry)
병진대칭이란 어떤 점을 어떤 방향을 직진 이동시킬 때 이동 후에도 그 점의 주의환경이 이전과 합동이 되게 하는 대칭요소이다. 쉽게 생각해서 도형을 x축 y축에 평행하게 이동시키는 것이다.
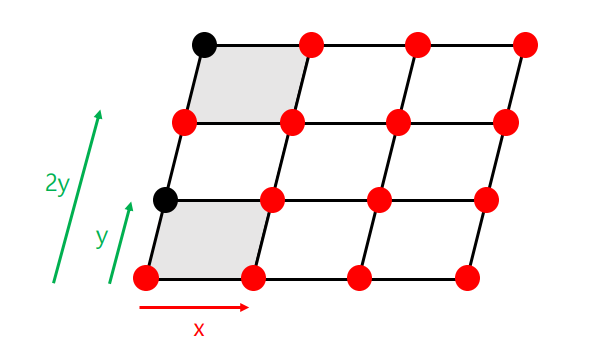
위에서 검은색 단위포는 y축 방향으로 2칸 이동했음에도 주변과 같다. 이때 x축 y축은 우리가 3차원에서 생각하는 공간이 아니라 단위포의 기저 벡터를 중심으로 생각해야 한다.
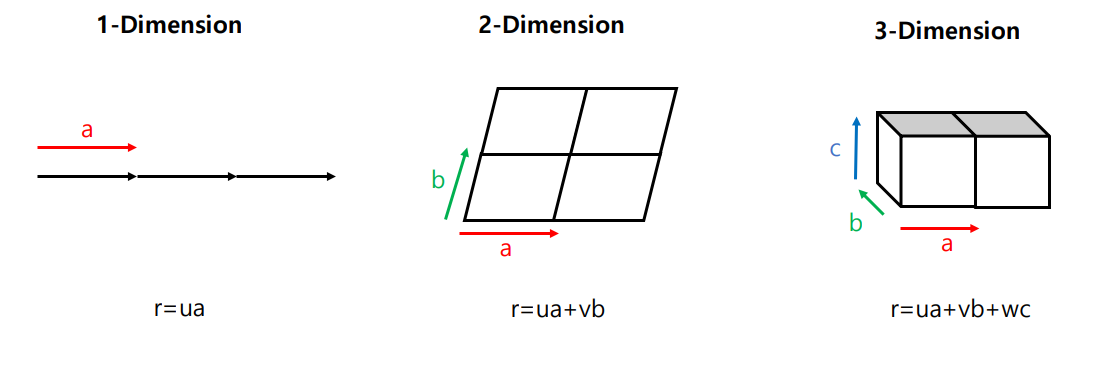
a,b,c 벡터는 격자점의 이동 방향과 크기를 나타내는 벡터중 가장 작은 크기의 벡터로 기본 격자 병진 벡터(fundamental translation vector)라고 한다. 병진벡터 r은 각 기본 격자에 정수배를 곱하고 더한 것이다.
2) 회전대칭(rotational symmetry)
회전대칭은 대칭점의 중심이나 회전축을 기준으로 일정 각도로 회전시킬때 회전 후에도 계속 합동이 되는 요소를 말한다. 위에서 보였던 회전변환이 전부 회전대칭에 들어간다.
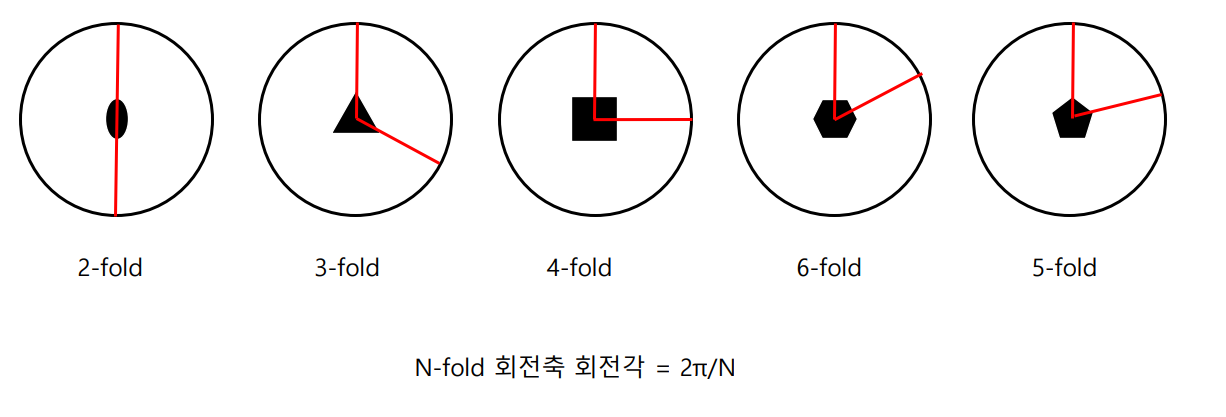
회전대칭은 몇번 회전시킬수 있는지(돌렸을때 몇번만에 처음으로 돌아오는지)를 기준으로 n-fold라고 부르며 n=4인 경우 4번 회전해서 원래 상태로 돌아온다. 기하학적으로 n은 정수인 어떤 값 (n=10이면 36도씩 10번 회전)도 가능하지만 실제 결정에서는 1,2,3,4,6-fold만 존재한다. 왜 그런지는 이후에 증명하게 된다. (5-fold도 이상적인 결정에서 존재하지 않는다. 하지만 셰흐트만 박사는 5-fold가 존재함을 증명해 노벨상을 받았다.이를 준결정이라고 한다)
4-fold 회전은 4번 회전하기에 (360/4=90) 회전각은 90도가 된다. 마찬가지로 N-fold 회전축에서 회전각은 360/N이 된다.
3) 경영대칭(mirror symmetry)
경영대칭은 어떤 면을 중심으로 면의 반대쪽 같은 거리만큼 이동시킬때 합동이 되는 대칭이다. 쉽게 생각하면 거울처럼 대칭이 되는 것이다. 그래서 표기 또한 두꺼운 검은 선과 mirror를 뜻하는 m을 표기한다. 만약 차트에서 진한 검은 선이 그어져 있다면 이건 자동적으로 mirror plane을 의미한다.
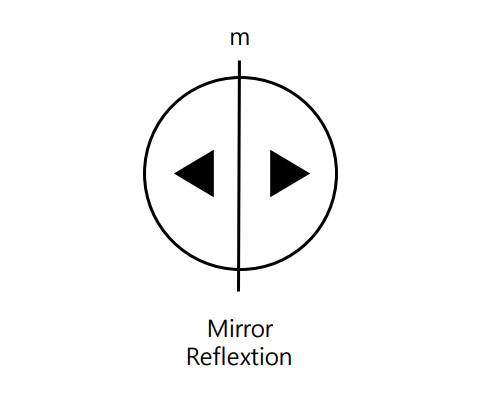
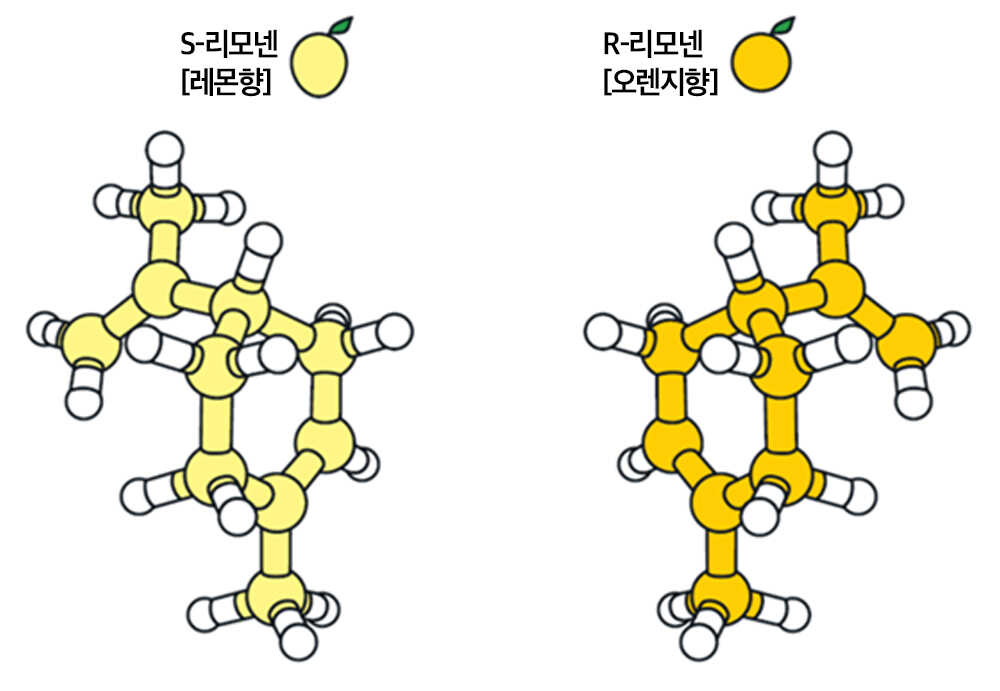
마치 화학의 키랄 분자와 똑같은 것이라 생각하면 된다. 키랄분자는 대표적인 경영대칭의 예다.
4) 반영대칭(inversion symmetry)
반영대칭이란 어떤 점에서 같은 거리이면서 그 점을 통하여 반대쪽으로 이동하였을때 합동이 되는 대칭을 의미한다. 쉽게 생각해서 한 점에 대한 대칭과 같은 것이다.
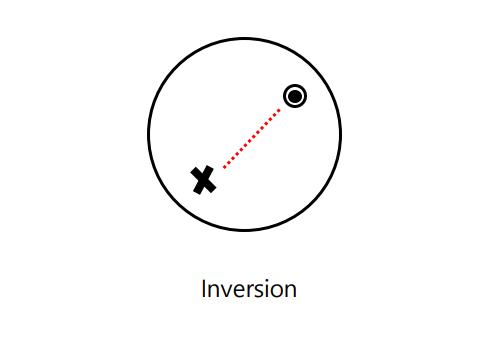
위의 그림에서 한 점은 구의 표면에 있고 경영대칭 된 점은 원점을 지나 반대편 원에 있다. 반영대칭은 회전 대칭축을 중심으로 180도 회전 후 회전 대칭구에 수직인 면으로 경영대칭을 한 것과 같다. 그래서 반영대칭은 회전대칭+경영대칭으로도 이해할 수 있다.
'재료공학 > 결정구조학' 카테고리의 다른 글
| 4. 7가지 기본격자와 브라베 격자 (0) | 2023.09.29 |
|---|---|
| 3. 공간상의 대칭 (5가지 회전 대칭) (0) | 2023.03.26 |
| 1. 격자와 단위포 (0) | 2023.03.21 |
| 규산염의 결정구조 (0) | 2021.06.12 |
| AmBnXz의 결정구조 (0) | 2021.06.11 |




