| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- X선 기초
- 결정구조학
- 분해전단응력
- X선의 발견
- laue
- 흡광
- X선 공학
- 3 o'clock things
- 빛의 손실
- 륀트겐
- von laue
- 재료과학
- 에너지 역학
- 화합물 반도체
- 라만 분석
- 슬립계
- 연속스펙트럼
- 전자의 속도
- drude
- 라만 분석기
- Raman
- 그루데 이론
- X선
- 일상
- 에디슨의 패배
- 결정립
- 전기장이 가해진
- 특성스펙트럼
- 라만 현상
- 재료열역학
- Today
- Total
공머생의 공부노트
4.1 7가지 기본격자와 브라베 격자 본문
1. 회전 대칭의 상호 결합
결정에 존재하는 회전대칭은 축을 기준으로 n만큼 회전이 가능하다. 앞선 포스팅에서 다루었듯 회전은 어느 각도로든 다 가능하지만 (https://yumy.tistory.com/98)단위셀이 무한히 반복된 격자 내에서는 병진 이동을 허용하는 1,2,3,4,6 중 회전만 허용된다. 하지만 실제 결정은 3차원 내에 존재하고 회전축이 항상 90*로 결합하는 2차원과 다르게 회전축은 어느 각으로도 결합이 가능하다.

하지만 여러개의 축이 항상 원하는 각도로 연결될 수 있는 것은 아니다. 평면에서 병진이동에 의해 대칭이 상쇄되어 가능한 회전이 제한된 것 처럼 여러개의 축들이 결합되며 대칭을 상쇄해버리기도 한다.
3차원의 공간에서 대칭축이 교차할때는 항상 3개의 축이 교차해야 하고 이들의 각도 관계에서도 제한이 가해진다. 사실 실제로 존재하는 공간 대칭의 수는 그리 많지 않다.
예를 들어 공간 상에서 6중 회전축과 2중 회전축 2개가 결합하는 상황을 생각하자.

만일 6중 회전축은 공간에서 z축 방향으로 존재하고 있고 360/6 = 60 회전시 그 모습이 같아져야 한다. 그러므로 2중 회전축도 6중 회전축이 성립하게 회전되야 하며 그 모든 축은 아래 그림과 같아질 것이다.

622 회전대칭에 우리가 임의의 축을 추가하여 6222축이라고 한다고 하더라도 이는 622 회전대칭의 모든 축중에 한개일 뿐이다. 전혀 이상한 위치에 2축을 생성한다면 6축 or 2축의 대칭성을 망가트리기에 존재할 수 없게 된다.
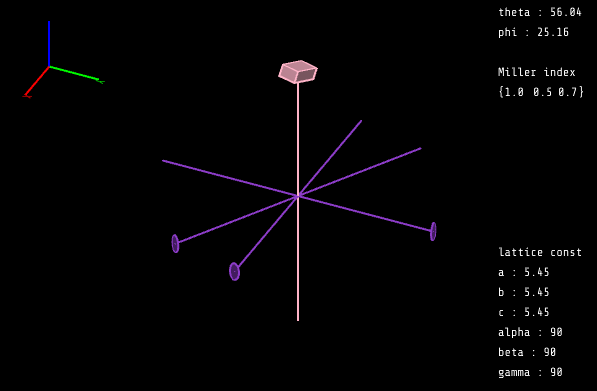
622 회전 대칭이 결정상에서 어떻게 존재하는지 확인할 수 있다. 아래의 시뮬레이션을 마우스로 드래그 하여 공간을 돌릴 수 있고 키보드에서 C를 누르면 정면으로 보이는 축에 대해 10*씩 회전이동 할 수 있다. R을 누르면 전체 설정이 리셋된다.
'재료공학 > 결정구조학' 카테고리의 다른 글
| SC, BCC, FCC의 역격자 공간 유도 (0) | 2024.07.02 |
|---|---|
| 4.2 7가지 기본격자와 브라베 격자 (0) | 2023.11.25 |
| 3. 공간상의 대칭 (5가지 회전 대칭) (0) | 2023.03.26 |
| 2. 대칭요소 (0) | 2023.03.26 |
| 1. 격자와 단위포 (0) | 2023.03.21 |




