| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- drude
- X선 기초
- 라만 분석기
- 에디슨의 패배
- X선
- 일상
- 결정구조학
- 특성스펙트럼
- Raman
- 전기장이 가해진
- 분해전단응력
- 에너지 역학
- 전자의 속도
- 그루데 이론
- laue
- von laue
- 흡광
- 결정립
- 재료열역학
- 빛의 손실
- 연속스펙트럼
- X선의 발견
- X선 공학
- 라만 현상
- 륀트겐
- 3 o'clock things
- 라만 분석
- 화합물 반도체
- 슬립계
- 재료과학
- Today
- Total
공머생의 공부노트
SAED diffraction 해석 4 (Ewald sphere) 본문
이제 사실상 거의 다왔다. 이전에 다루었던 회절의 원리를 바탕으로 이제는 실제로 SAED 패턴을 해석해야 한다.


우리가 해야하는 것은 미지의 spot pattern이 존재하고 이 물질의 구성이나 상을 알고 있을때 이로부터 그 물질의 격자상수, 결정계 등을 파악해야 한다.
SAED 패턴 해석의 장점은 전자빔이 시편의 아주 작은 국부적 영역을 비추기에 물질의 나노스케일에서의 작은 결정계 차이도 추적할 수 있다는 점이다. (분석비가 치솟는건 덤이다)
1. Ewald Sphere
우선 ewald sphere라는 것에 대해 이해해야 한다. 우선 3번 포스팅에서 보았던 이미지를 다시 떠올려 보면
SAED diffraction 해석 3 (회절의 원리)
SAED 패턴은 TEM에서 가속된 전자가 시편을 만났을 때 회절함으로서 발생한다. 가속된 전자는 마치 X선 처럼 물질을 만나 경로가 꺾이고 이때 틀어진 경로의 전자들이 SAED 패턴의 점을 만든다. 일
yumy.tistory.com
전자 빔이 격자를 가진 시편을 투과하며 일부가 회절하는 것을 생각해보자
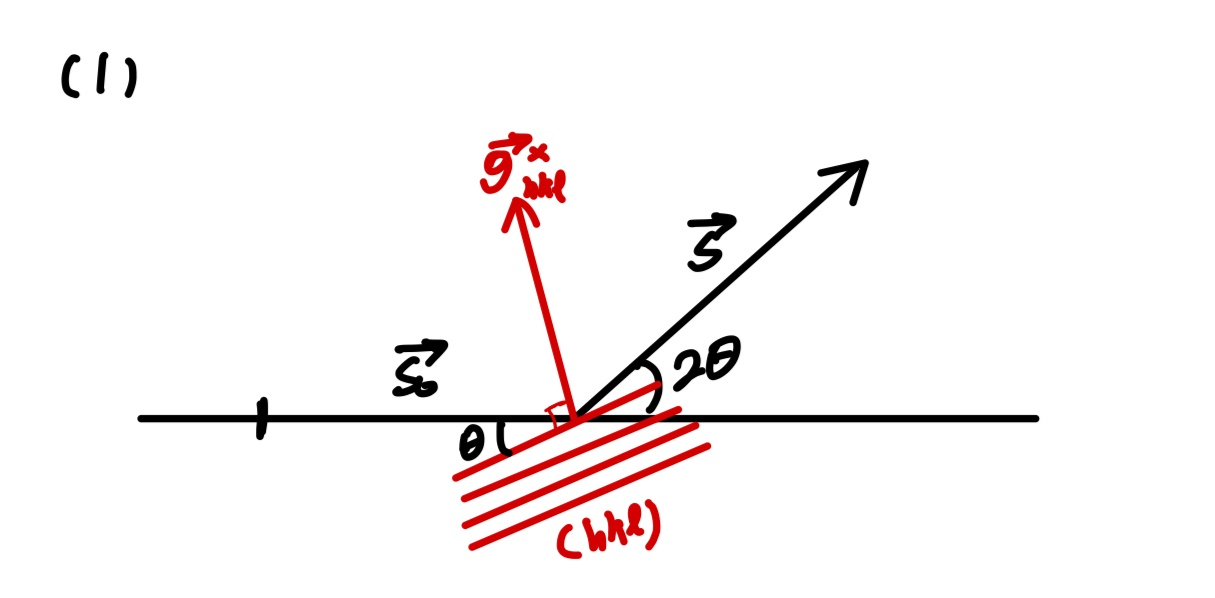
이때 회절이 일어나는 조건은 S-So 벡터가 g* 벡터와 같아질 때 발생한다는 것을 우리는 알고 있다. g* 역격자 벡터는 결정의 특정면을 나타낸다고 생각하면 된다. (그림에서 hkl 면에 수직한 벡터가 된다) (왜 그런지 모른다면 1,2,3 포스팅을 참고해야 한다)
그럼 회절이 일어나는 상황을 모두 찾으려면 두 벡터가 같아지는 상황을 찾으면 되는 것이다.
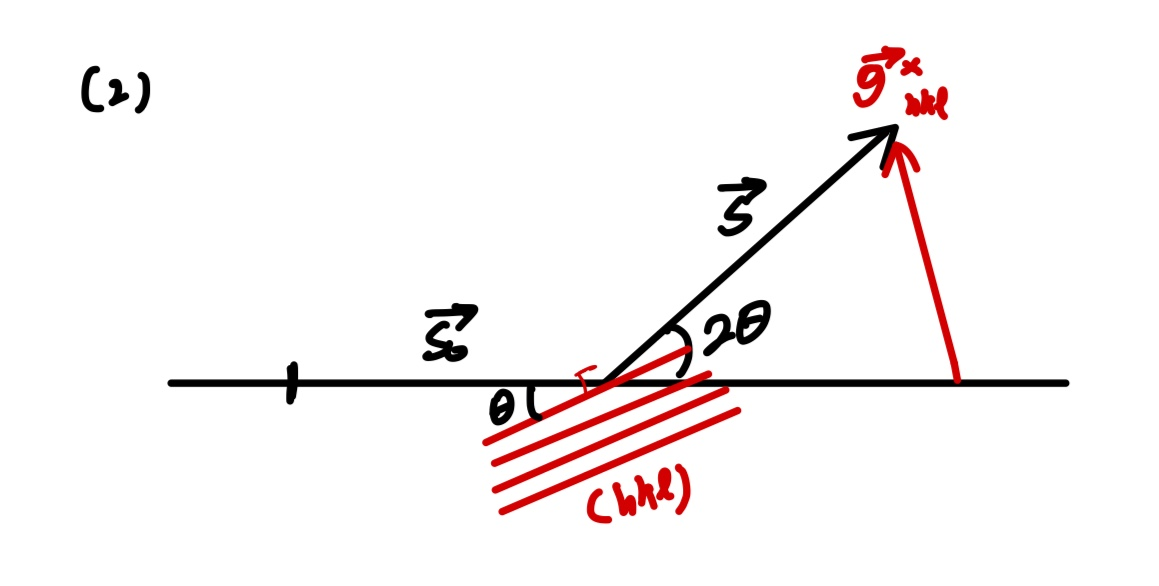
이제 g벡터를 (역격자 벡터)를 평행이동시켜 2번 그림같이 만들어보자. 벡터는 평행이동시켜도 온전히 같은 벡터이므로 아무런 문제가 없다.
이때 두 벡터가 같은 경우를 찾기 위해서 시편을 중심으로 원을 그려본다면?
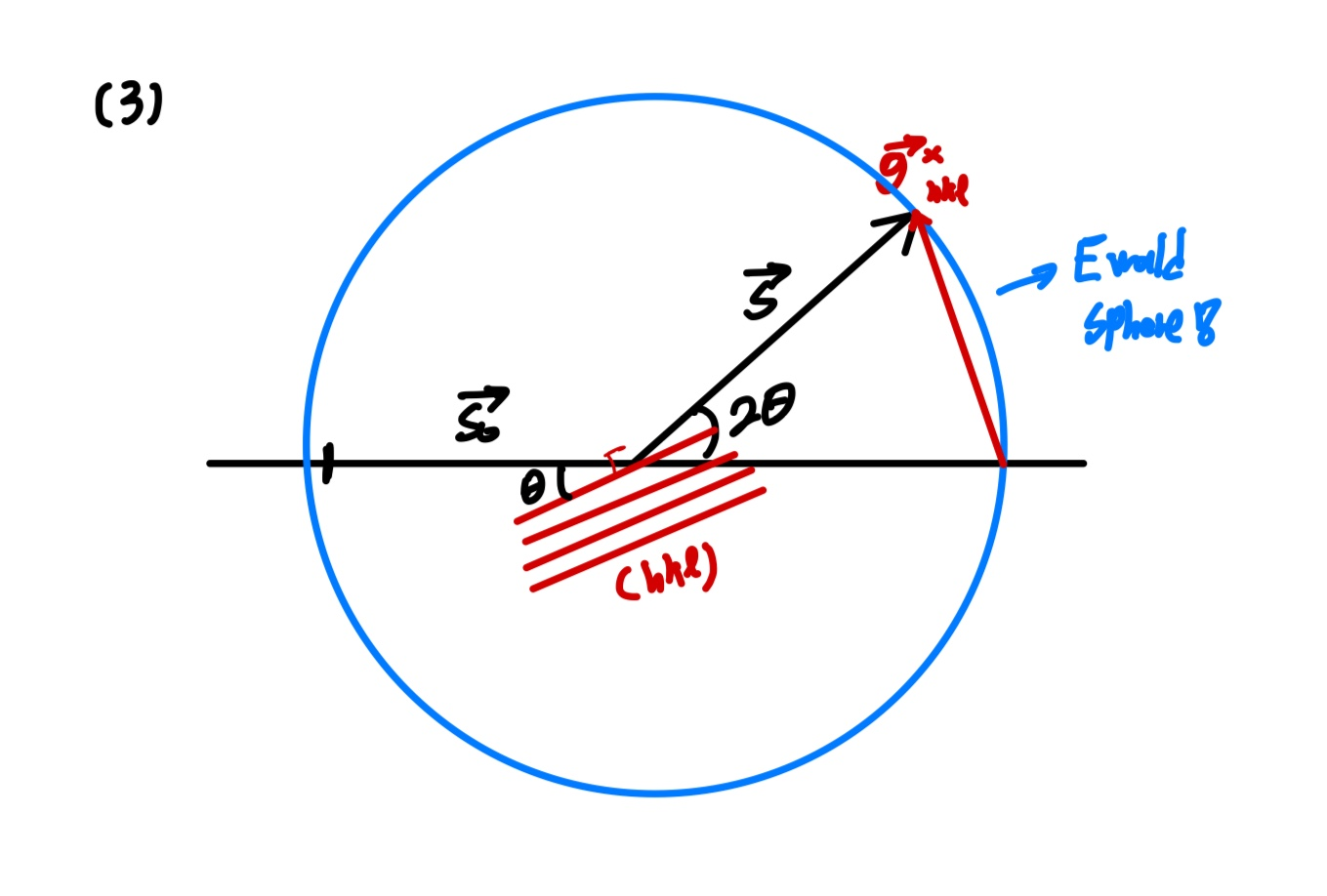
이것이 바로 ewald sphere가 되며 역격자 벡터가 ewald sphere와 만나는 그 지점은 회절이 발생하는 지점이 된다. 역격자 벡터의 길이가 짧거나 방향이 달라서 만나지 않는다면 그 면은 회절하지 않는 것이다.
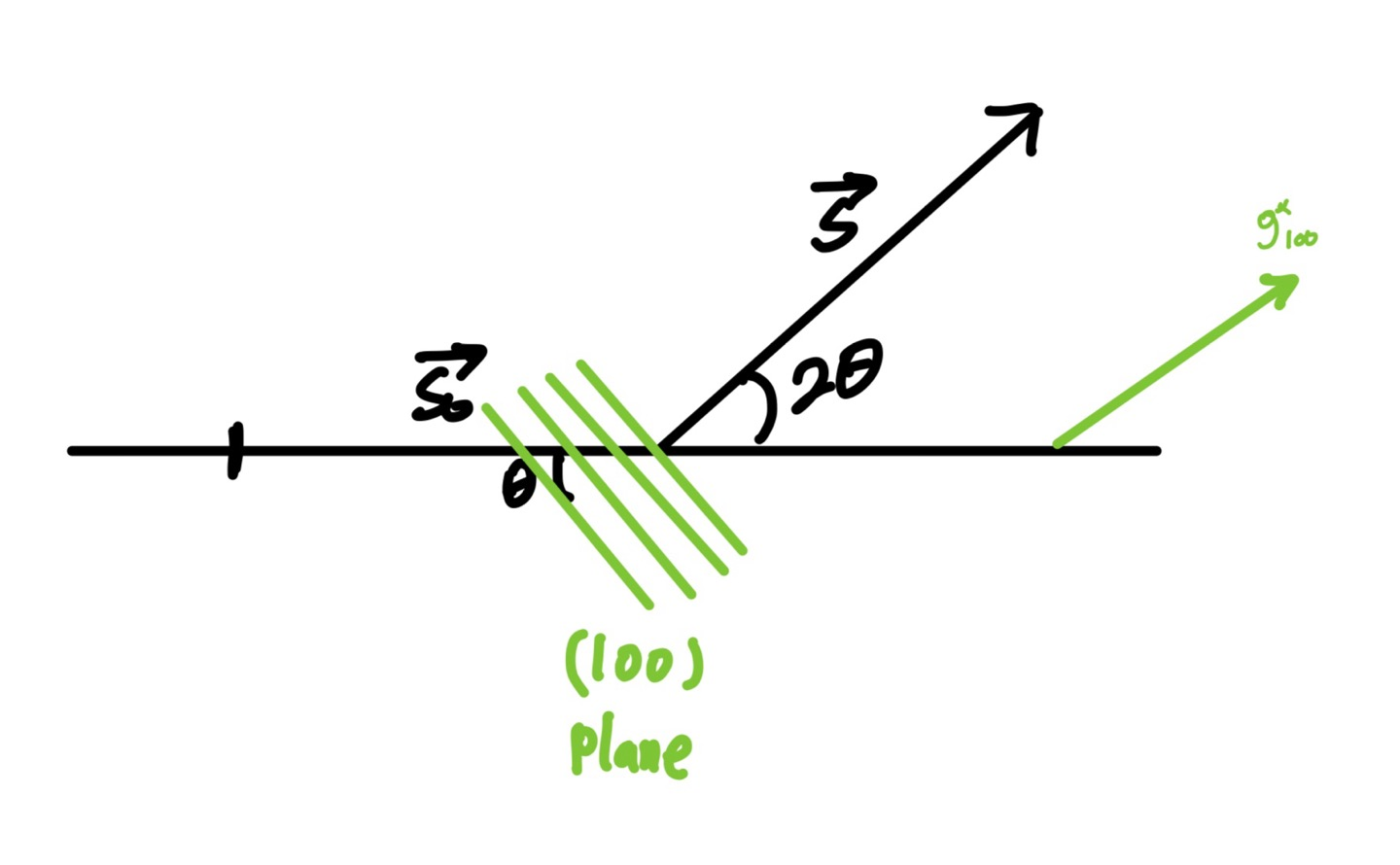
다음과 같이 임의의 면에 의한 역격자 벡터가 있다고 가정해 보자. 실제로 S-So벡터와 만나지도 않는다.
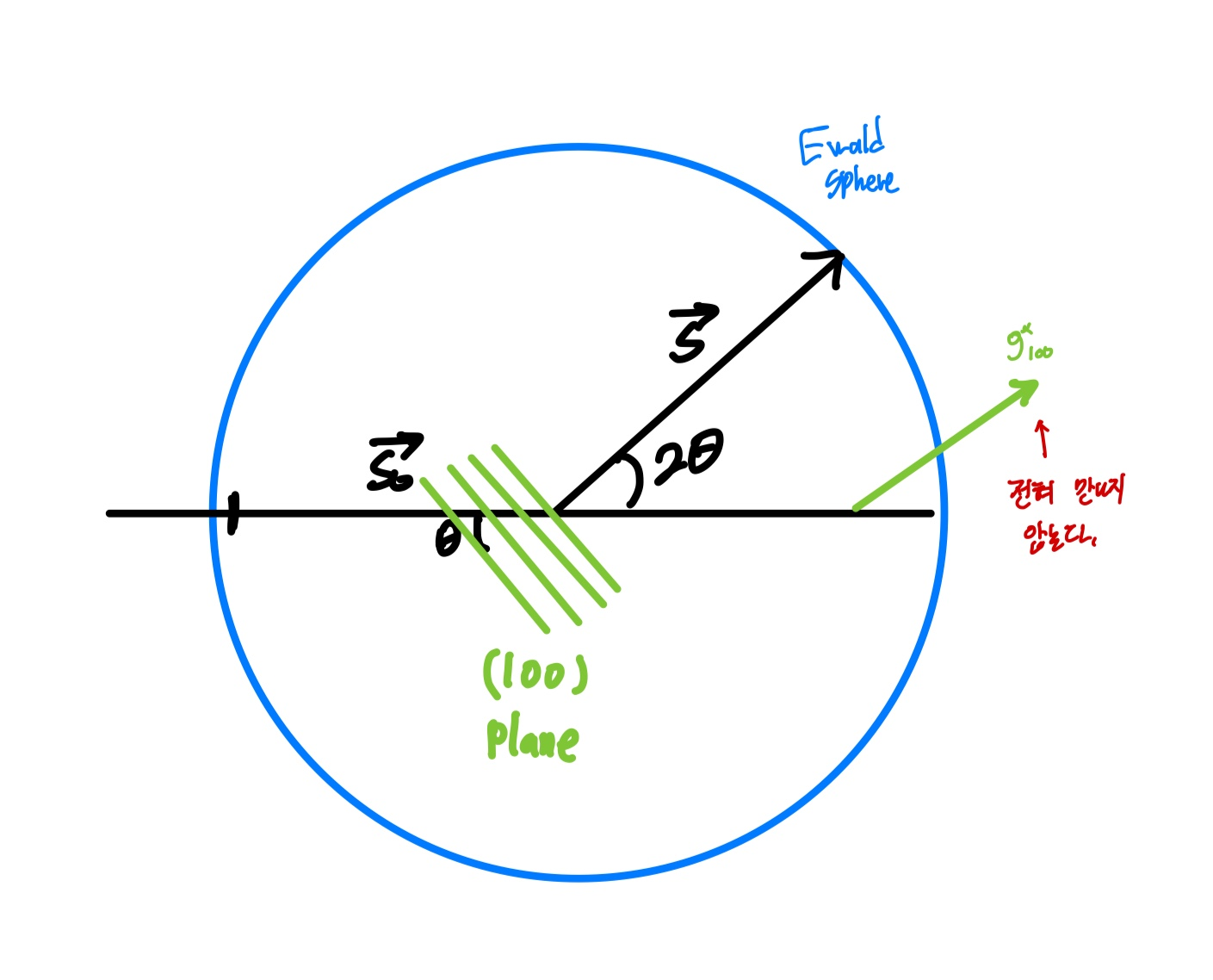
이를 ewald 공간에서 본다면 g*(100)는 에발드 구와 전혀 만나지 않는다. 즉 전자빔의 S벡터가 저렇게 꺾일 이유가 없으며 이는 회절이 전혀 일어나지 않고 투과만 될 것을 예상 가능하다.
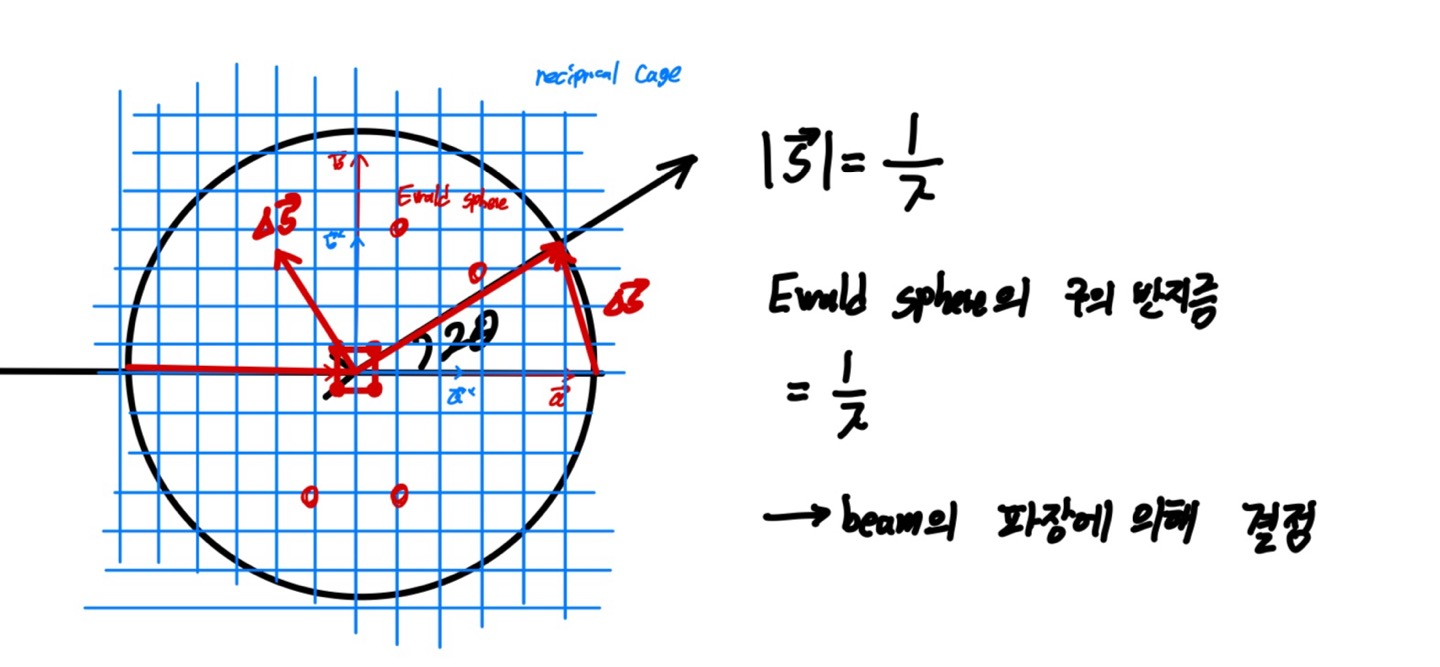
이때 ewald 구의 반지름 길이는 S벡터의 길이인 입사파의 파장의 역수가 된다. 만일 입사빔의 가속이 커져서 파장이 짧아지면 sphere는 점점더 커진다. 또한 ewald구는 역격자와 동일한 공간에 존재한다. 즉 일반적인 공간의 길이가 아닌 역격자의 역공간에 존재하는 것이다.
2. Camera Constant
TEM의 SAED를 해석할 때는 위의 ewald 구에 의해 계산되는 회절 가능한 점을 파악하는게 전부다.
하지만 역격자와 ewald구는 실제 공간에 존재하지 않는다. 실제 공간에서 긴건 역격자 공간에서 짧아지는 관계를 가진다. 심지어는 결정구조에 따라 관계가 아예 달라진다.
이를 위해서 우리는 TEM에서 보이는 pattern의 실제 공간의 길이를 재고 이를 역격자 공간에서의 길이로 변환해야 한다.
그러기 위해서는 TEM에서 Camera Constant를 알아야 하고 이를 바탕으로 변환해야 한다.
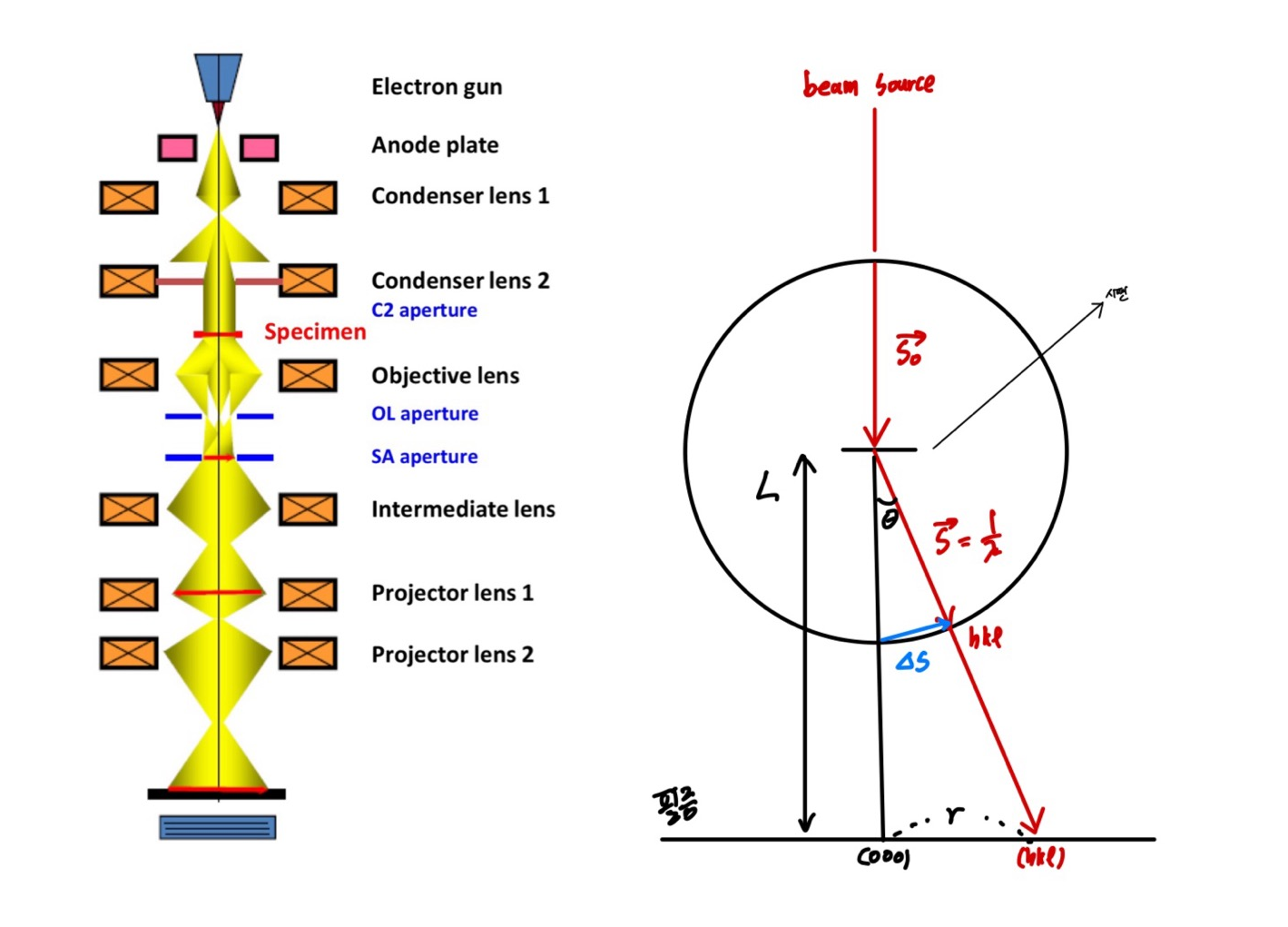
위의 Ewald 공간을 가로로 90정도만 돌려보자. 그렇다면 TEM에서 전자빔이 회절되어 필름에 도달하는 것을 쉽게 상상해볼 수 있을 것이다.
Camera Constant는 쉽게 생각해서 전자빔의 이동 경로를 바탕으로 실제 공간 vs 역격자 공간의 길이비를 만드는 것이다. 우리가 실공간에서 1cm라고 측정한다면 이를 Camera Constant를 바탕으로 역격자 공간에서의 길이를 알 수 있다.
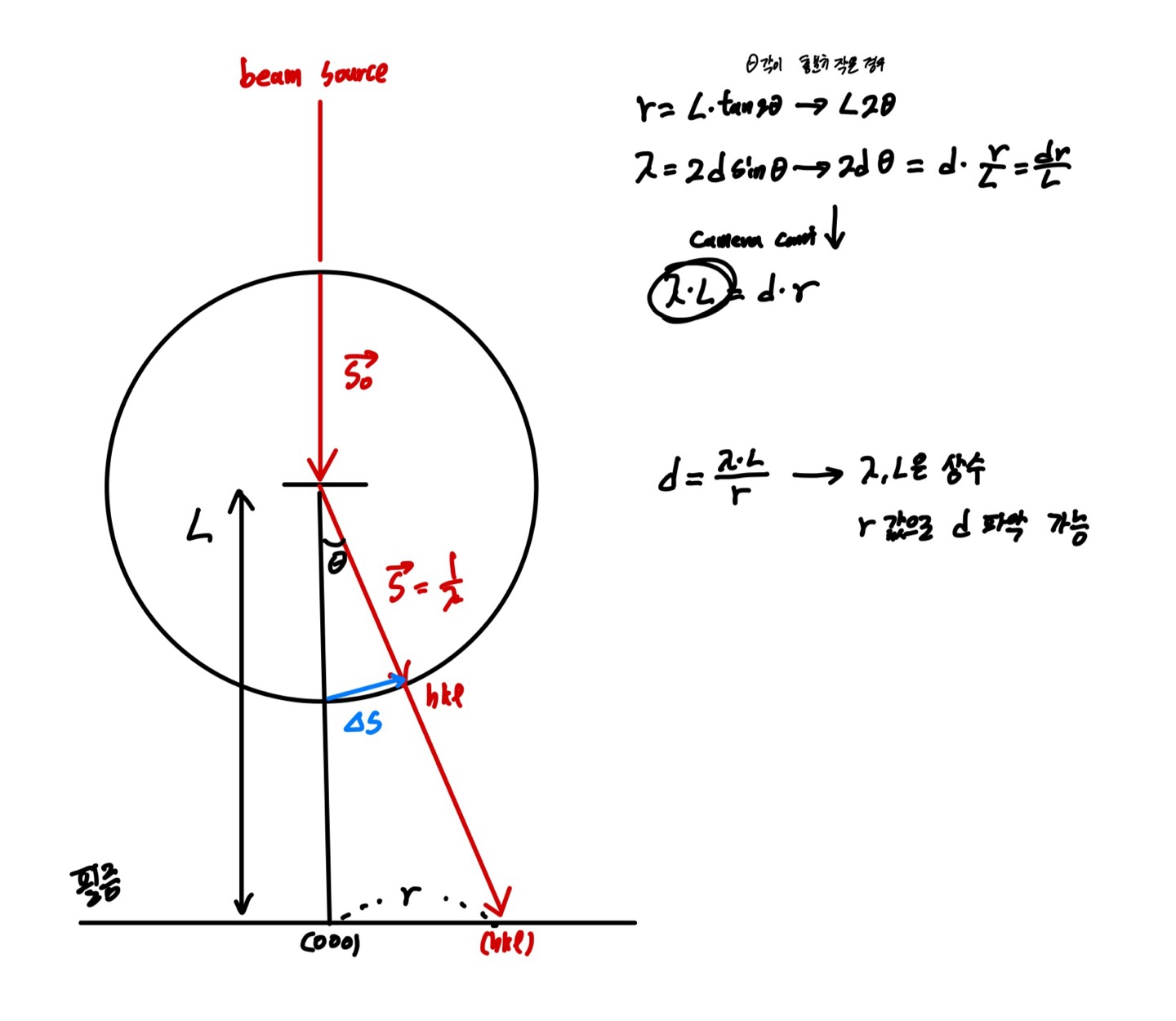
일반적으로 TEM의 전자빔의 가속이 매우 크기에 전자빔의 파장은 매우 짧고 ewald 구의 크기는 매우 크다. 그렇기에 delta의 값은 매우 작고 tanx에서 x가 매우 작을때 tanx = x로 근사할 수 있으므로
직각 삼각형 계산에 따라 Camera Constant공식이 얻어진다.
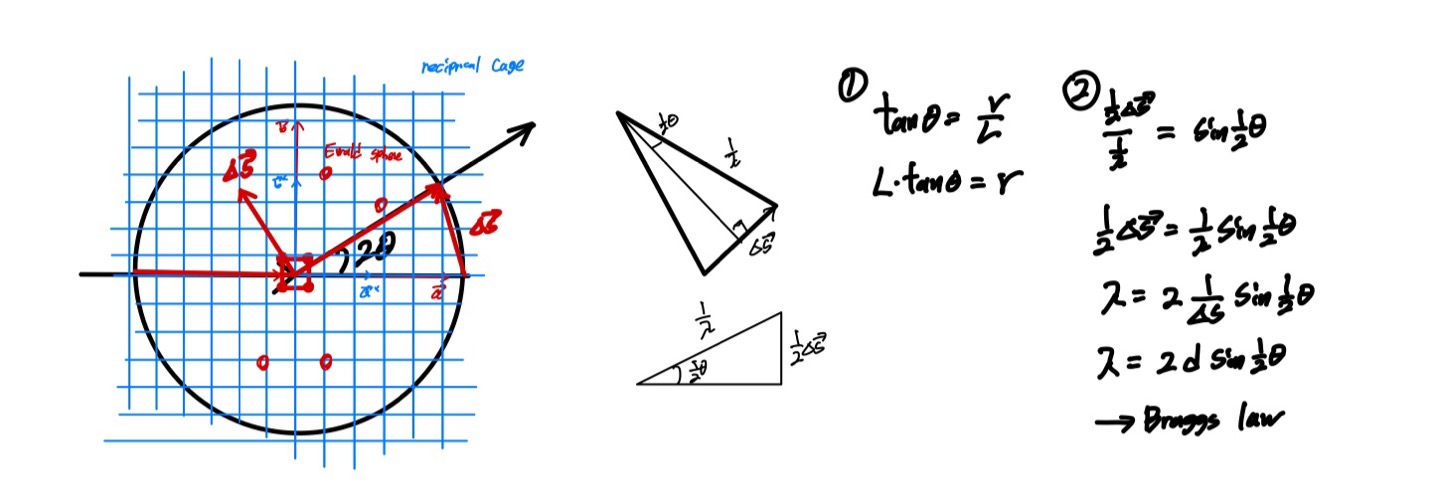
간단한 관계식을 통해서 역으로 브래그 법칙을 얻어낼 수도 있다.
Camera Constant는 보통 기기마다 정해지며 특정 상수 값으로 주어진다.
'연구 분석법 > SEM, TEM 분석법' 카테고리의 다른 글
| SAED diffraction 해석 5 (Spot pattern indexing) (0) | 2025.03.22 |
|---|---|
| SAED diffraction 해석 3 (회절의 원리) (2) | 2024.07.17 |
| SAED diffraction 해석 2 (역격자의 정의) (1) | 2024.07.01 |
| SAED diffraction 해석 1 (0) | 2024.07.01 |
| EELS 분석 1 (1) | 2024.06.11 |




