| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 에너지 역학
- 결정구조학
- 라만 분석기
- 화합물 반도체
- 일상
- 륀트겐
- 슬립계
- 라만 현상
- 연속스펙트럼
- laue
- 결정립
- X선
- 에디슨의 패배
- 전기장이 가해진
- 빛의 손실
- 라만 분석
- X선 기초
- X선 공학
- 분해전단응력
- 3 o'clock things
- 재료과학
- von laue
- 재료열역학
- X선의 발견
- 그루데 이론
- 흡광
- Raman
- drude
- 특성스펙트럼
- 전자의 속도
- Today
- Total
공머생의 공부노트
SAED diffraction 해석 2 (역격자의 정의) 본문
SAED diffraction 해석 1에서는 간단히 SAED의 원리에 대해 다루고 무엇을 해야하는지에 대해 이야기 했으며, 다음 포스팅에서부터는 회절에 의한 일반적인 원리와 인덱싱을 위한 기초 지식을 다룰 계획입니다. 만일 해석법에 대해 바로 보고 싶다면 "SAED diffraction 해석 4"를 참고해주기 바랍니다.
하지만 올바른 해석을 위해 2, 3편의 내용 또한 필수적이니 필요한 순간에 다시 돌아오면 도움이 될 것이라도 확신합니다. (만일 기기분석을 듣는다면 이 한문제를 포기하지 않길 바랍니다, 문제를 풀기 위해서는 1,4편의 내용만 보는걸 추천합니다)
1. 역격자와 결정

결정의 unit cell 원자의 배열중에 가장 작은 단위를 통해 정의하고 이를 통해 우리는 결정의 기본 벡터를 정의하게 된다. 결정의 기본병진벡터는 결정계에 따라 다르며 일종의 정의이기에 반드시 수학적으로 엄밀하게 정의되지 않아도 된다.
이에 따라 우리는 단결정 내부에서 위치를 기본 병진 벡터의 결합으로 설명할 수 있다. 이건 가장 기본적인 결정에서의 정의가 된다.
이때 역격자(reciprocal lattice)는 실공간에 존재하는 격자의 단위벡터를 연산하여 얻어지는 가상의 격자로서 실제 공간에 존재하지는 않지만 회절 공간에 존재하며 실격자로부터 유도된다. 즉 실격자의 constant와 vector가 바뀌면 역격자도 따라서 변한다.

역격자는 위에 식으로 유도되며 이 값에 따라 서로 다른 결정의 역격자가 생성된다.

위의 정의에 따라 역격자는 본인을 제외한 실격자가 이루는 평면에 대해 무조건 수직한다는 점을 알 수 있고 실격자와 위와 같은 관계를 가진다. (나중에 중요하게 쓰인다)

앞에서 정의된 역격자는 임의의 상수 h, k, l을 붙여 역격자 벡터로서 역격자 공간에서 해석하는데, 이때 역격자 공간은 회절 조건 혹은 고체물리에서는 k space로 해석된다. h, k, l 이 결정학에서 면을 나타내는 기호와 똑같이 사용되는건 우연이 아니다.
2. 실제 공간과 역격자 사이의 관계
위의 역격자와 실공간 사이의 관계를 통해 실제 공간의 결정 구조에 따라 역격자의 형태 또한 달라진다는 점을 알 수 있다. 실제 수학적인 유도를 통해 알아보면 Simple cubic은 그대로 SC로 역격자 벡터가 형성되고, BCC는 FCC로 역격자를 생성하며, FCC는 BCC로 역격자를 형성한다.
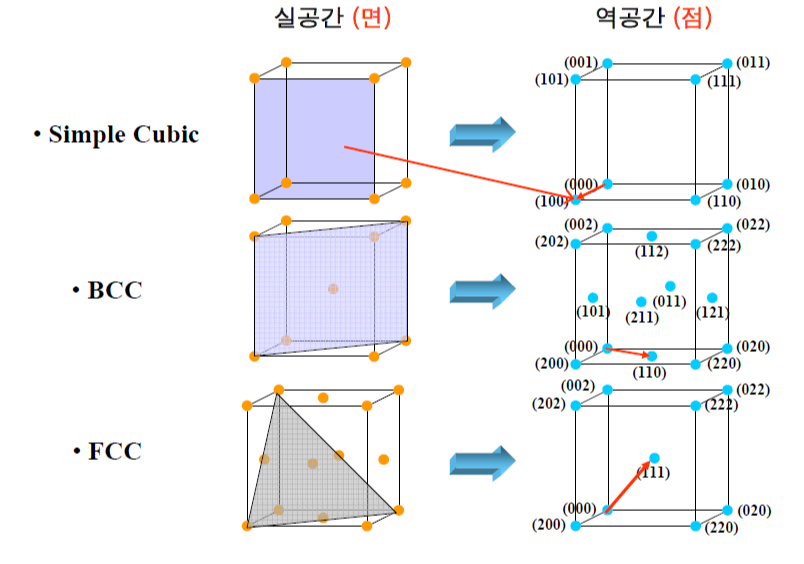
실제 SAED 패턴을 해석할때는 이점이 가장 중요하다. 시편의 실공간에서의 회절에 따라 역격자 공간도 똑같은 각도로 회전할 수 있고 그때 패턴의 모양은 SC, BCC, FCC가 구분이 어려워지는 경우가 있다. 이때 역격자의 생성이 각 결정구조에 따라 다르다는 것을 이해하면 도움이 된다.
SC, BCC, FCC의 역격자 공간 유도
1. SC의 역격자 공간simple cubic은 기본 벡터가 직교좌표계와 유사하며 모두 서로 직교한다는 특징을 가진다. 하지만 벡터의 크기는 a이다. 역격자 관계로부터 역격자의 크기는 1/a가 되며 방향은
yumy.tistory.com
왜 역격자 공간에서 BCC가 FCC가 되고 FCC가 BCC가 되는지에 대한 설명은 위의 포스팅에서 수식을 따라가며 이해하면 된다. 어렵다면 실제로 그렇게 된다는 것을 이해하면 된다.
3. 역격자의 길이 관계
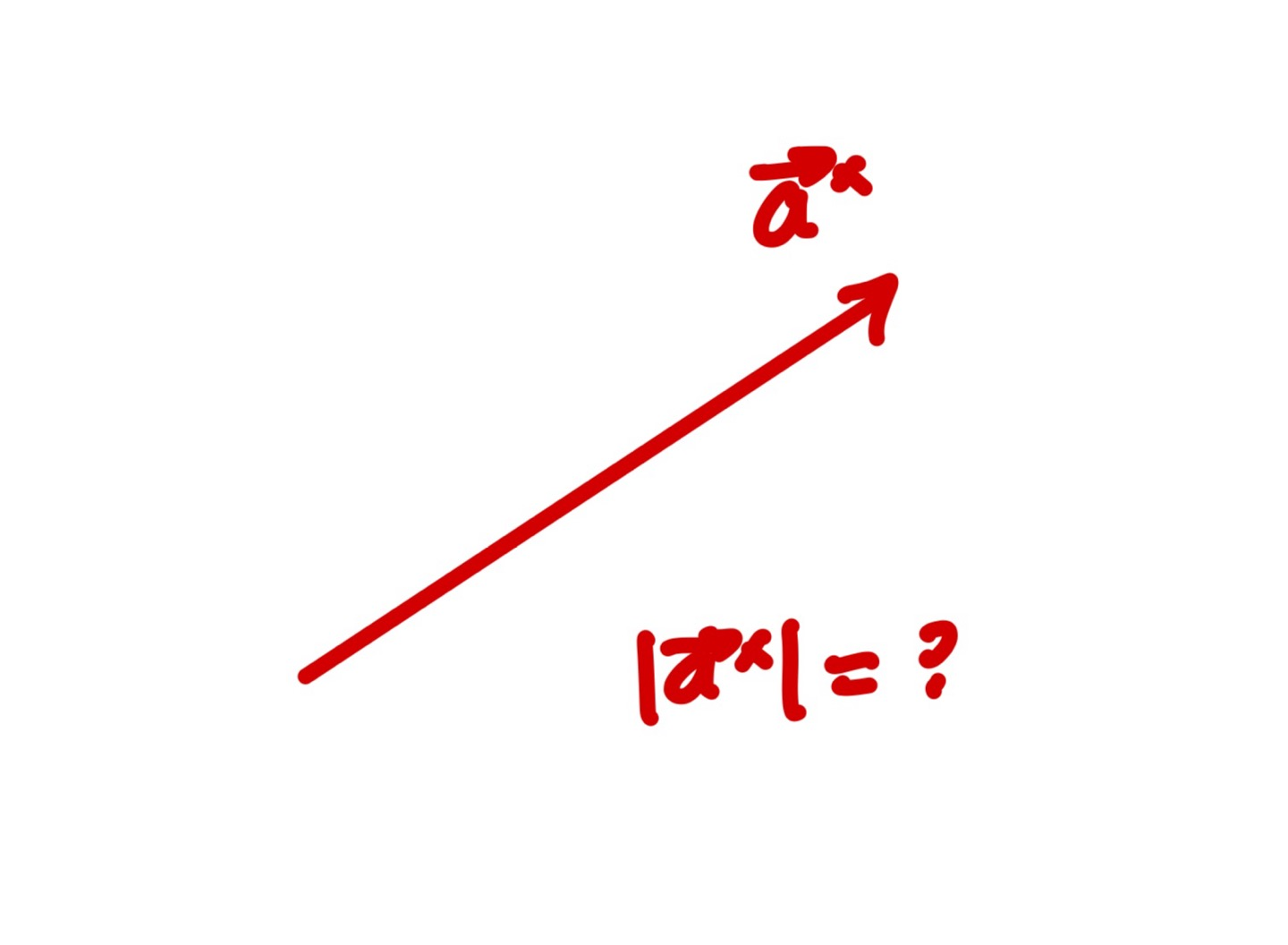
우선 어떠한 결정계에서든 a* 벡터의 길이를 알고 싶다고 한다면 이는 생각보다 간단하지 않다.
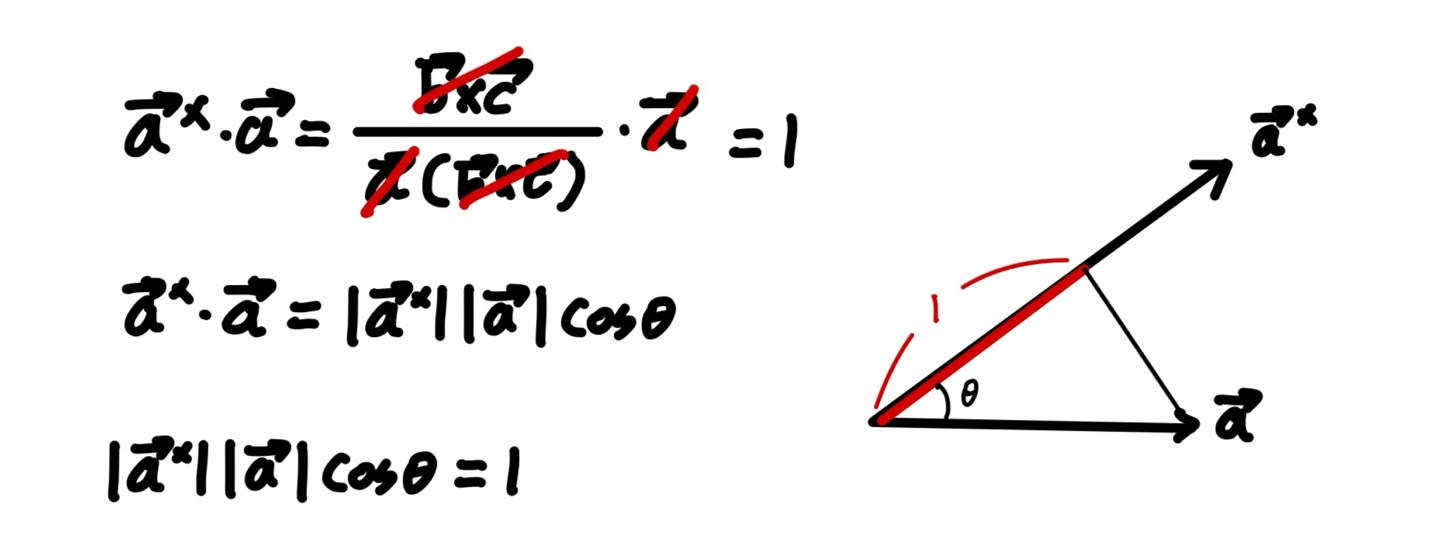
가장 기본적인 가정인 a와 a*벡터의 곱이 1이라는 것에서 시작한다면 당연하게도 어떤 결정계에서도 a와 a*의 스칼라 곱은 1이 된다. 이때 a와 a*벡터는 결정계에 따라 일정한 각도만큼 틀어져 있을 수 있다.
a와 a*벡터의 스칼라곱 정의를 이용하면 a와 a*의 곱이 1임을 이용하여 길이와 각도에 대한 공식을 유도할 수 있다. 이 공식은 a*벡터와 a벡터의 정사형이 항상 1의 길이를 가진다는 의미이다.
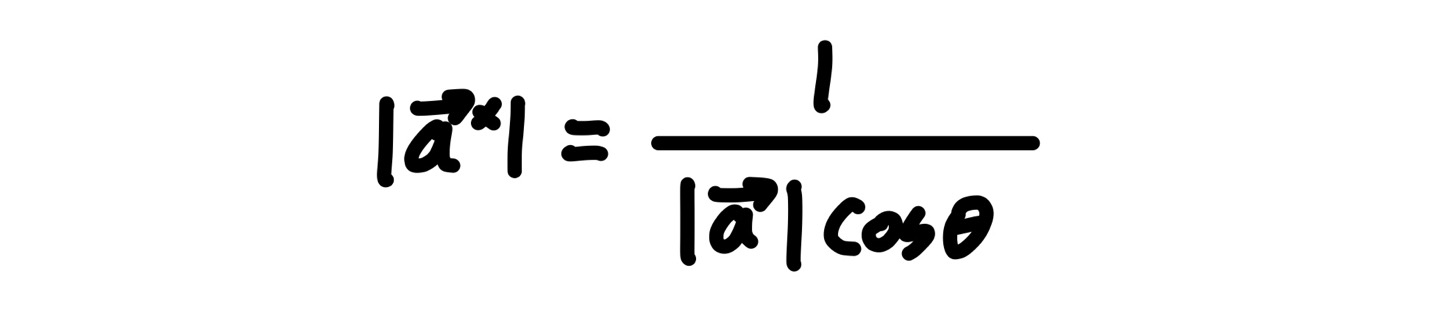
a*의 길이를 구하기 위해서는 a와 두 벡터 사이에 각도를 알아야 하는데, 우선 a의 경우 격자 상수이기에 쉽게 적용하여 값을 구할 수 있다.
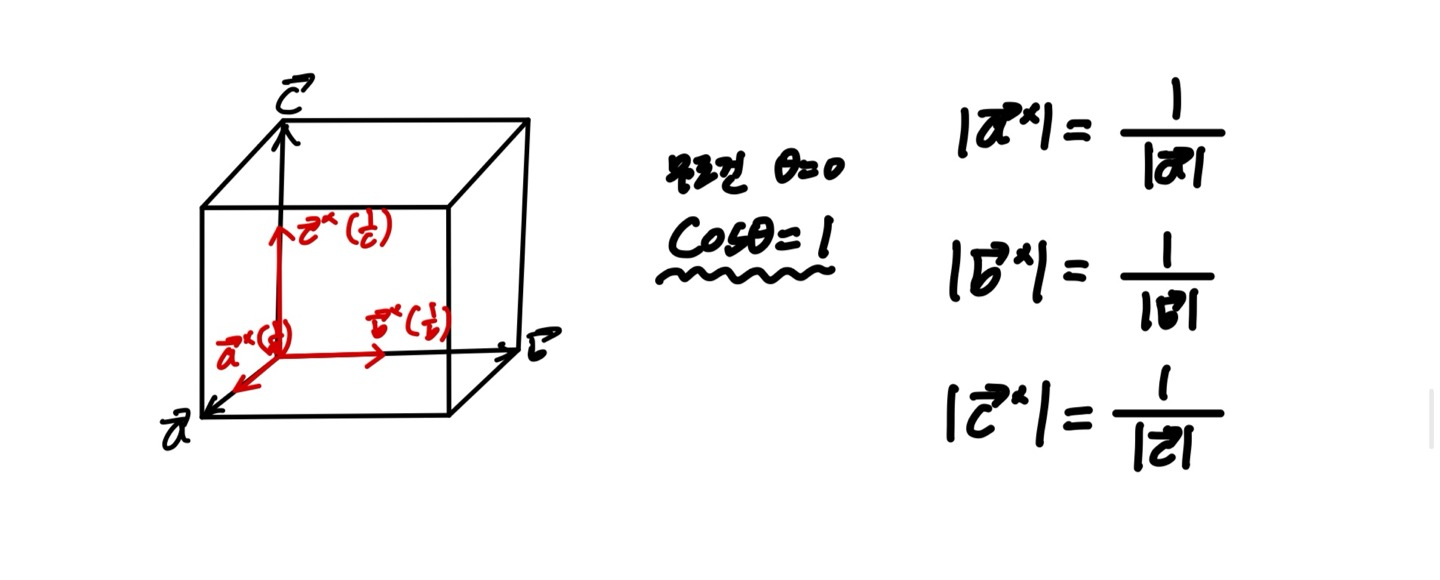
직교좌표계의 경우 두 벡터의 방향은 항상 같고 역격자 벡터의 길이는 항상 격자 상수의 역수가 된다.
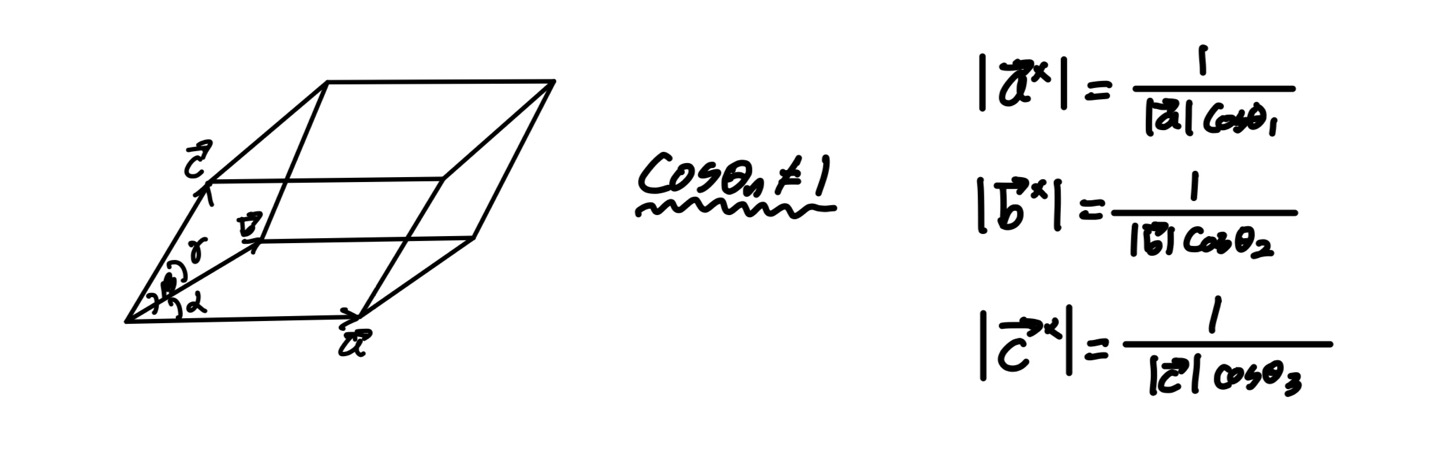
하지만 직교좌표계가 아닐 경우 cos값은 알수 없고 단순히 격자 상수의 역수로 이해하기는 불가하다. 이를 풀어내기 위해서는 역격자의 정의에서 절댓값을 취하여 기하적으로 접근할 필요가 있다.
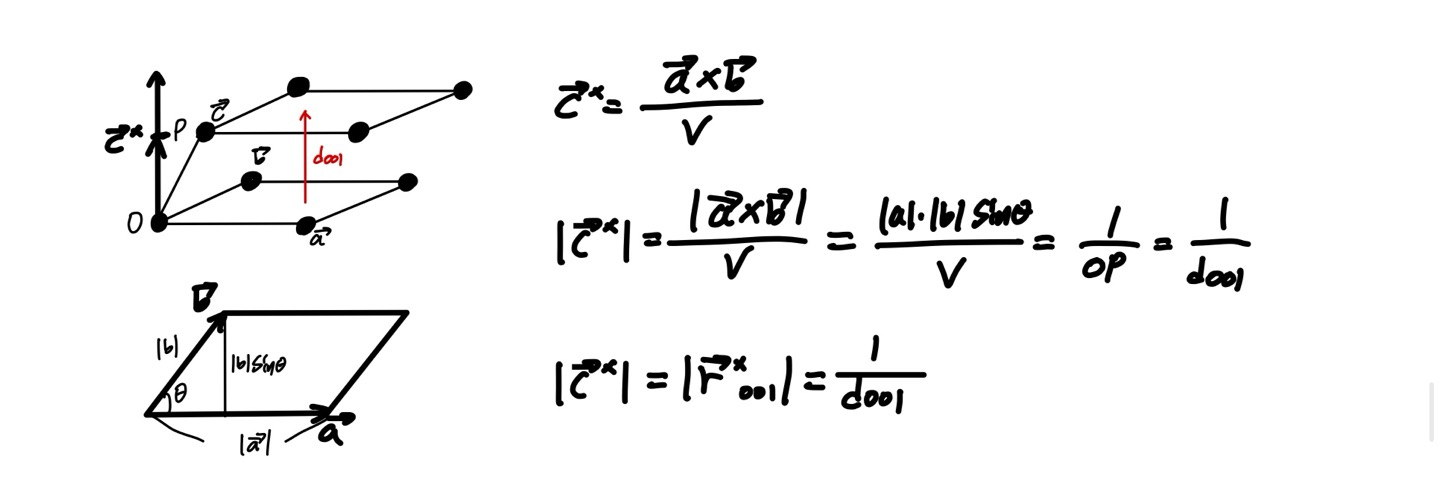
c*벡터의 길이를 구하고자 한다면 V는 상수가 되기에 빠져나가고 결국 a와b의 외적에서 a*b*sin값을 구하면 되는데 이는 실공간에서 a와 b가 이루는 unit cell의 평행사변형의 넓이가 된다. 부피를 면의 넓이로 나누면 높이가 되고 이는 c 결정 격자 방향으로의 면간의 거리가 된다.
이때 가장 기본 정의에서 a와 b가 이루는 평면에 c*는 무조건 수직하기에 높이인 OP는 c*에 평행한 길이가 된다. 결국 OP는 001방향의 면간거리가 된다.
모든 경우에서 역격자 벡터의 길이는 면간 거리의 역수가 된다.
'연구 분석법 > SEM, TEM 분석법' 카테고리의 다른 글
| SAED diffraction 해석 5 (Spot pattern indexing) (0) | 2025.03.22 |
|---|---|
| SAED diffraction 해석 4 (Ewald sphere) (0) | 2024.07.17 |
| SAED diffraction 해석 3 (회절의 원리) (2) | 2024.07.17 |
| SAED diffraction 해석 1 (0) | 2024.07.01 |
| EELS 분석 1 (1) | 2024.06.11 |




