| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 화합물 반도체
- 연속스펙트럼
- 그루데 이론
- 분해전단응력
- 특성스펙트럼
- 결정립
- X선의 발견
- 흡광
- von laue
- Raman
- drude
- 라만 분석
- 륀트겐
- 에디슨의 패배
- 슬립계
- 라만 분석기
- 재료열역학
- 재료과학
- X선 공학
- 전자의 속도
- 3 o'clock things
- 전기장이 가해진
- 일상
- X선 기초
- X선
- 빛의 손실
- 에너지 역학
- 라만 현상
- 결정구조학
- laue
- Today
- Total
공머생의 공부노트
원자에 의한 X선의 산란 (scattering by atom) 본문
전자에 의한 X선의 산란 (scattering by electron)
공간을 진행하는 X선은 재료에 입사되면 산란을 일으킨다. 산란이란 "빛이 미립자에 부딪혔을 때, 방향을 바꾸어 여러 방면으로 흩어지는 현상" 인데, 즉 말 그대로 X선이 재료에 의해 퍼지는 것
yumy.tistory.com
앞선 포스팅에서 전자기파인 X선이 전자에 의해 산란되는 것을 파동방정식으로 일반화 하였다. 하지만 우리가 실질적으로 물질에 대해 생각할 때는 전자 1개가 아닌 원자의 단위에서 생각할 필요가 있다.
원자와 전자밀도함수의 정의

물질을 자세히 분해해보면 수많은 결정이 복잡하게 결합된 Bulk상태에서, 원자가 입자립 내에서 정돈된 Crystal 상태, 더 확대하면 원자핵과 전자로 이루어진 atom의 상태로 해석할 수 있다.
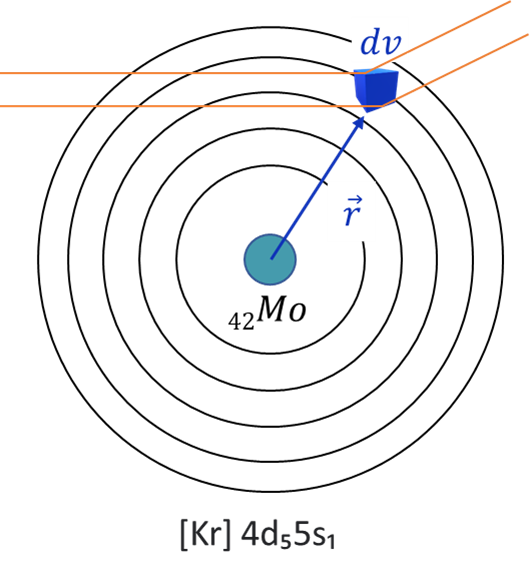
즉 물질이 무엇으로 이루어져 있는지는 가장 기본적인 단계인 원소에서 결정되는 것이다 (엄밀히 원자는 가장 기본적인 형태는 아니다). 이러한 원소들은 원자 핵의 전하에 따라 같은 수의 전자를 가지게 되고 이것이 주기율표의 주기성을 만드는 주된 원인이 된다. 예를 들어 Mo원소는 42개의 원자핵을 가지며 동시에 42개의 전자를 원자핵 주변에 포함하고 있다.
앞선 포스팅에서 설명한대로 X선은 전자에 의해 회절한다. 그 말은 원자 내에 존재하는 42개의 전자에 의해 X선이 회절할 수 있다는 의미이다. 원자 내부에는 중성자와 양성자도 존재하지만 질량이 상대적으로 매우 무거워 전자에 비해서는 그 영향력이 작다. (이 또한 이후 포스팅에서 다룰 예정)
이론적으로 존재하는 측정의 오차 (불확정성의 원리) 때문에 전자의 위치와 운동량을 동시에 유도해 내는 것은 불가능하지만 슈레딩거의 방정식을 활용한 확률적인 접근으로 전자의 영향을 계산할 수 있다.

위의 ρ(r) 함수는 원자 내에의 r 벡터 위치에서의 매우 작은 부피 dv에 전자가 존재할 확률을 나타낸다. 이를 전자 밀도 함수라고 하며 양자역학적으로 해석하여 구해 내기도 하고 회절된 패턴을 역으로 분석하여 알아내기도 한다. 우리가 이 함수를 직접 유도해내야 할 필요는 일단 없으므로 그저 어떤 것인지만 이해하고 지나가자.
ρ(r)(전자밀도)함수는 r의 위치의 dv의 크기에서 전자가 존재할 확률이다
즉, 단위 부피당 전자의 개수이다
전자에 의해 X선이 회절되는 것을 파악 했던 것과 동일한 방식을 사용하여 원자에 대해 회절되는 것을 풀어내면 된다.
원자에 의한 X선의 회절
위에서 정의한 대로 전자밀도함수는 r 벡터에 dv 미소부피 내에 존재하는 전자의 밀도이다. 그렇기에 ρ(r)*dv는 r벡터 위치에 있는 전자의 개수가 되고 전자 n개에 의한 회절 방정식을 적용할 수 있다.
수식을 그대로 적용하여 r에서의 회절 방정식을 얻어내고 r에 대한 구를 적분하여 원자 전체에서의 방정식을 유도해 내면 아래와 같다.

방정식에서 파동에 의한 부분을 제외하면 전자에 의해서 얻어진 것 처럼 산란진폭을 얻어낼 수 있다. 만일 여러분이 원자에 대해 완벽한 ρ(r)를 가지고 있다면 아래 식에 적용하여 어떤 벡터각도에서 회절이 발생하고 그 정도는 얼마인지 알아낼 수 있다.

'재료공학 > X-선 회절공학' 카테고리의 다른 글
| 기본적인 파동방정식의 일반화 (3) | 2022.01.18 |
|---|---|
| 전자에 의한 X선의 산란 (scattering by electron) (1) | 2021.09.20 |
| X선의 흡광 (Absorbption) (0) | 2021.09.20 |
| X선의 발생 (0) | 2021.09.19 |
| X선의 성질 (0) | 2021.09.19 |




